Second Order Probabilities for Uncertain and Conflicting Evidence
Paper and Code
Mar 27, 2013
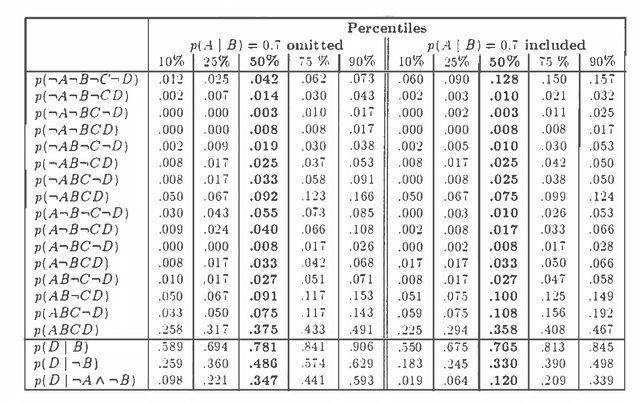
In this paper the elicitation of probabilities from human experts is considered as a measurement process, which may be disturbed by random 'measurement noise'. Using Bayesian concepts a second order probability distribution is derived reflecting the uncertainty of the input probabilities. The algorithm is based on an approximate sample representation of the basic probabilities. This sample is continuously modified by a stochastic simulation procedure, the Metropolis algorithm, such that the sequence of successive samples corresponds to the desired posterior distribution. The procedure is able to combine inconsistent probabilities according to their reliability and is applicable to general inference networks with arbitrary structure. Dempster-Shafer probability mass functions may be included using specific measurement distributions. The properties of the approach are demonstrated by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge