Search-based Methods to Bound Diagnostic Probabilities in Very Large Belief Nets
Paper and Code
Mar 20, 2013


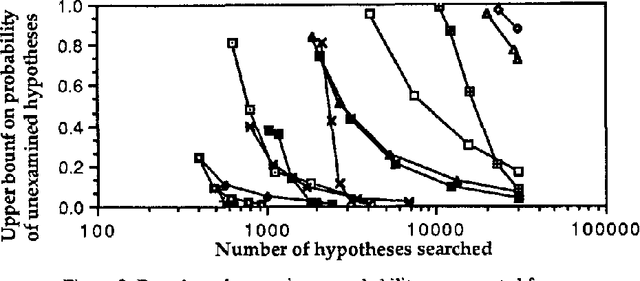
Since exact probabilistic inference is intractable in general for large multiply connected belief nets, approximate methods are required. A promising approach is to use heuristic search among hypotheses (instantiations of the network) to find the most probable ones, as in the TopN algorithm. Search is based on the relative probabilities of hypotheses which are efficient to compute. Given upper and lower bounds on the relative probability of partial hypotheses, it is possible to obtain bounds on the absolute probabilities of hypotheses. Best-first search aimed at reducing the maximum error progressively narrows the bounds as more hypotheses are examined. Here, qualitative probabilistic analysis is employed to obtain bounds on the relative probability of partial hypotheses for the BN20 class of networks networks and a generalization replacing the noisy OR assumption by negative synergy. The approach is illustrated by application to a very large belief network, QMR-BN, which is a reformulation of the Internist-1 system for diagnosis in internal medicine.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge