Score and Information for Recursive Exponential Models with Incomplete Data
Paper and Code
Feb 06, 2013
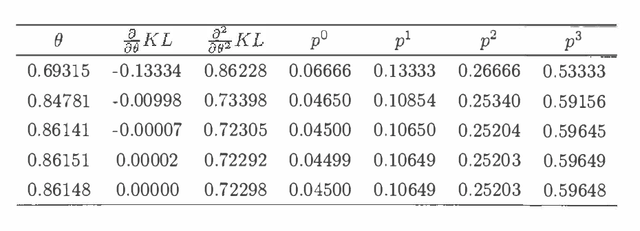
Recursive graphical models usually underlie the statistical modelling concerning probabilistic expert systems based on Bayesian networks. This paper defines a version of these models, denoted as recursive exponential models, which have evolved by the desire to impose sophisticated domain knowledge onto local fragments of a model. Besides the structural knowledge, as specified by a given model, the statistical modelling may also include expert opinion about the values of parameters in the model. It is shown how to translate imprecise expert knowledge into approximately conjugate prior distributions. Based on possibly incomplete data, the score and the observed information are derived for these models. This accounts for both the traditional score and observed information, derived as derivatives of the log-likelihood, and the posterior score and observed information, derived as derivatives of the log-posterior distribution. Throughout the paper the specialization into recursive graphical models is accounted for by a simple example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge