Scheduling for Urban Air Mobility using Safe Learning
Paper and Code
Sep 28, 2022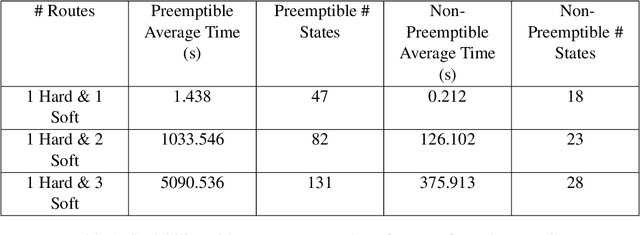

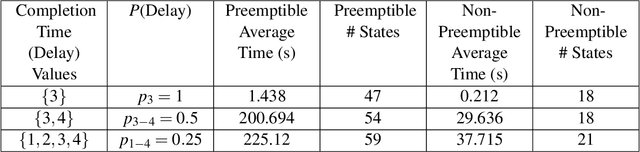
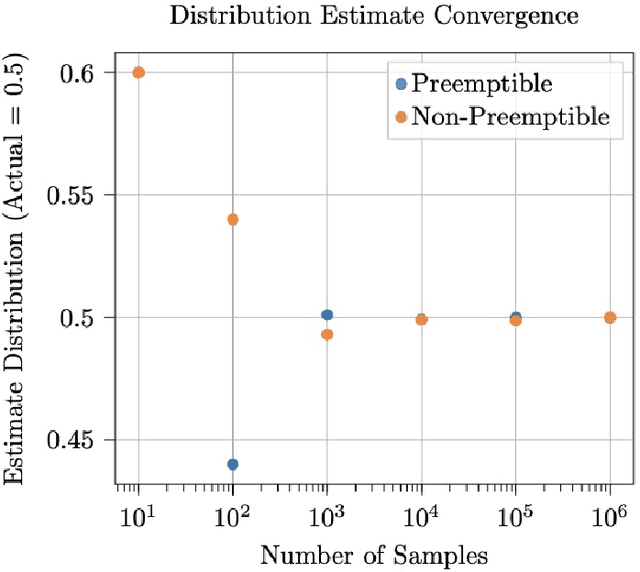
This work considers the scheduling problem for Urban Air Mobility (UAM) vehicles travelling between origin-destination pairs with both hard and soft trip deadlines. Each route is described by a discrete probability distribution over trip completion times (or delay) and over inter-arrival times of requests (or demand) for the route along with a fixed hard or soft deadline. Soft deadlines carry a cost that is incurred when the deadline is missed. An online, safe scheduler is developed that ensures that hard deadlines are never missed, and that average cost of missing soft deadlines is minimized. The system is modelled as a Markov Decision Process (MDP) and safe model-based learning is used to find the probabilistic distributions over route delays and demand. Monte Carlo Tree Search (MCTS) Earliest Deadline First (EDF) is used to safely explore the learned models in an online fashion and develop a near-optimal non-preemptive scheduling policy. These results are compared with Value Iteration (VI) and MCTS (Random) scheduling solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge