Scaling Laws for Reward Model Overoptimization
Paper and Code
Oct 19, 2022
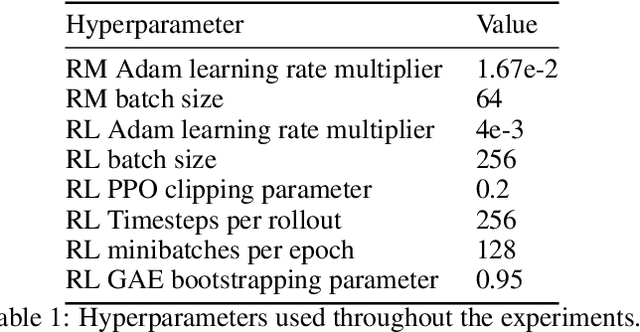


In reinforcement learning from human feedback, it is common to optimize against a reward model trained to predict human preferences. Because the reward model is an imperfect proxy, optimizing its value too much can hinder ground truth performance, in accordance with Goodhart's law. This effect has been frequently observed, but not carefully measured due to the expense of collecting human preference data. In this work, we use a synthetic setup in which a fixed "gold-standard" reward model plays the role of humans, providing labels used to train a proxy reward model. We study how the gold reward model score changes as we optimize against the proxy reward model using either reinforcement learning or best-of-$n$ sampling. We find that this relationship follows a different functional form depending on the method of optimization, and that in both cases its coefficients scale smoothly with the number of reward model parameters. We also study the effect on this relationship of the size of the reward model dataset, the number of reward model and policy parameters, and the coefficient of the KL penalty added to the reward in the reinforcement learning setup. We explore the implications of these empirical results for theoretical considerations in AI alignment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge