Scalable Kernel Learning via the Discriminant Information

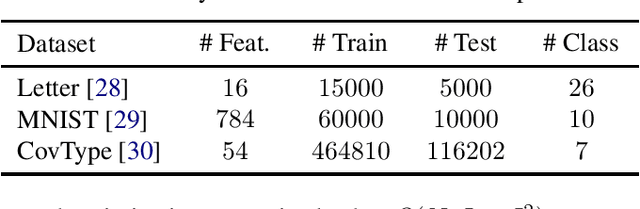
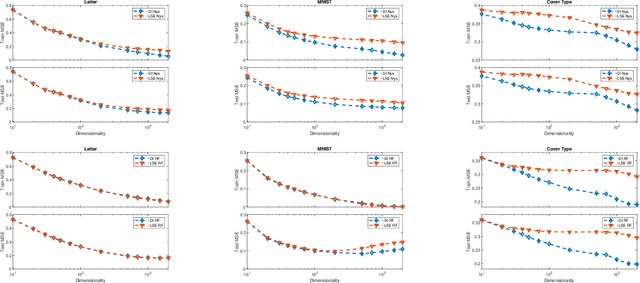
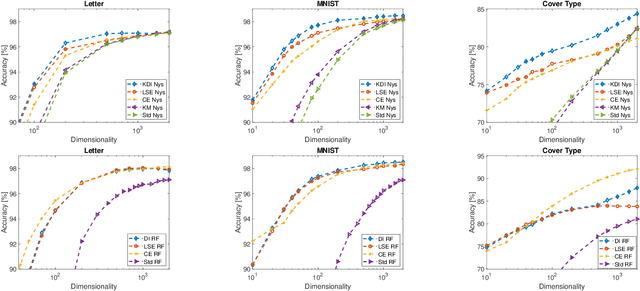
Kernel approximation methods have been popular techniques for scalable kernel based learning. They create explicit, low-dimensional kernel feature maps to deal with the high computational and memory complexity of standard techniques. This work studies a supervised kernel learning methodology to optimize such mappings. We utilize the Discriminant Information criterion, a measure of class separability, which is extended to cover a wider range of kernels. By exploiting the connection of this criterion to the minimum Kernel Ridge Regression loss, we propose a novel training strategy that is especially suitable for stochastic gradient methods, allowing kernel optimization to scale to large datasets. Experimental results on 3 datasets showcase that our techniques can improve optimization and generalization performances over state of the art kernel learning methods.