Scalable Distributed Planning for Multi-Robot, Multi-Target Tracking
Paper and Code
Jul 18, 2021
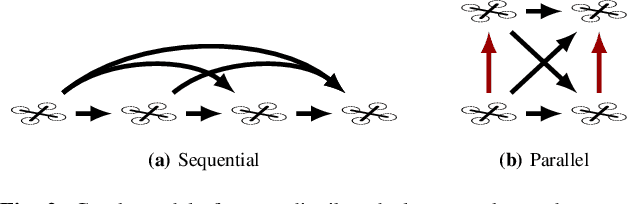
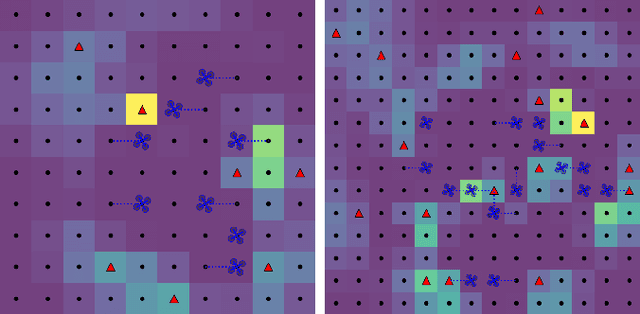

In multi-robot multi-target tracking, robots coordinate to monitor groups of targets moving about an environment. We approach planning for such scenarios by formulating a receding-horizon, multi-robot sensing problem with a mutual information objective. Such problems are NP-Hard in general. Yet, our objective is submodular which enables certain greedy planners to guarantee constant-factor suboptimality. However, these greedy planners require robots to plan their actions in sequence, one robot at a time, so planning time is at least proportional to the number of robots. Solving these problems becomes intractable for large teams, even for distributed implementations. Our prior work proposed a distributed planner (RSP) which reduces this number of sequential steps to a constant, even for large numbers of robots, by allowing robots to plan in parallel while ignoring some of each others' decisions. Although that analysis is not applicable to target tracking, we prove a similar guarantee, that RSP planning approaches performance guarantees for fully sequential planners, by employing a novel bound which takes advantage of the independence of target motions to quantify effective redundancy between robots' observations and actions. Further, we present analysis that explicitly accounts for features of practical implementations including approximations to the objective and anytime planning. Simulation results -- available via open source release -- for target tracking with ranging sensors demonstrate that our planners consistently approach the performance of sequential planning (in terms of position uncertainty) given only 2--8 planning steps and for as many as 96 robots with a 24x reduction in the number of sequential steps in planning. Thus, this work makes planning for multi-robot target tracking tractable at much larger scales than before, for practical planners and general tracking problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge