Sampling Random Group Fair Rankings

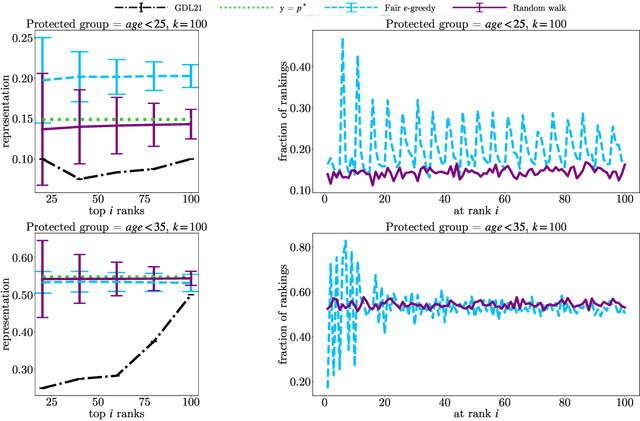
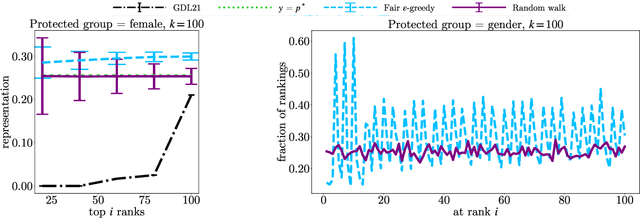
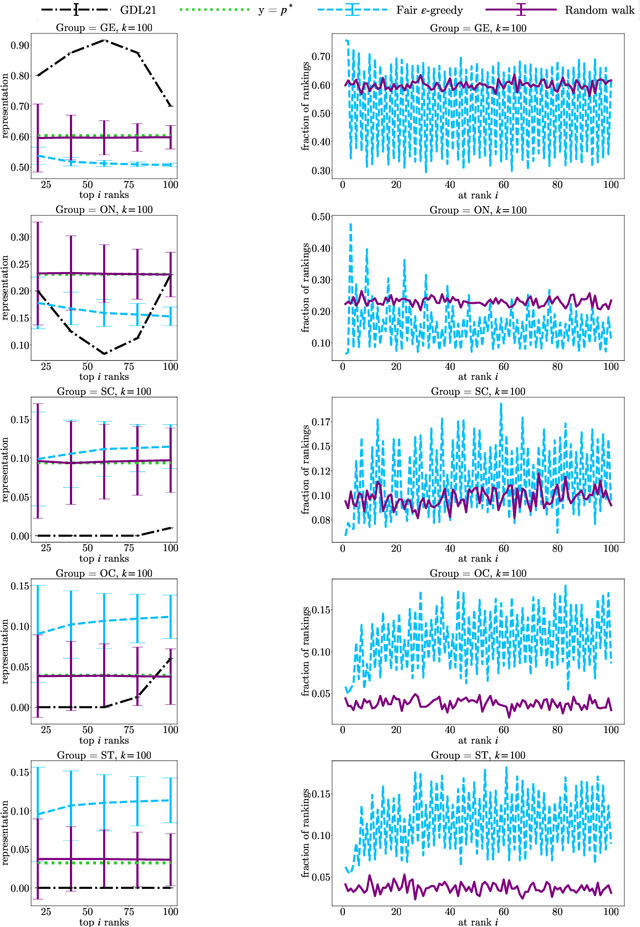
In this paper, we consider the problem of randomized group fair ranking that merges given ranked list of items from different sensitive demographic groups while satisfying given lower and upper bounds on the representation of each group in the top ranks. Our randomized group fair ranking formulation works even when there is implicit bias, incomplete relevance information, or when only ordinal ranking is available instead of relevance scores or utility values. We take an axiomatic approach and show that there is a unique distribution $\mathcal{D}$ to sample a random group fair ranking that satisfies a natural set of consistency and fairness axioms. Moreover, $\mathcal{D}$ satisfies representation constraints for every group at every rank, a characteristic that cannot be satisfied by any deterministic ranking. We propose three algorithms to sample a random group fair ranking from $\mathcal{D}$. Our first algorithm samples rankings from $\mathcal{D}$ exactly, in time exponential in the number of groups. Our second algorithm samples random group fair rankings from $\mathcal{D}$ exactly and is faster than the first algorithm when the gap between upper and lower bounds on the representation for each group is small. Our third algorithm samples rankings from a distribution $\epsilon$-close to $\mathcal{D}$ in total variation distance, and has expected running time polynomial in all input parameters and $1/\epsilon$ when there is a large gap between upper and lower bound representation constraints for all the groups. We experimentally validate the above guarantees of our algorithms for group fairness in top ranks and representation in every rank on real-world data sets.