Safe Online Convex Optimization with Unknown Linear Safety Constraints
Paper and Code
Nov 14, 2021
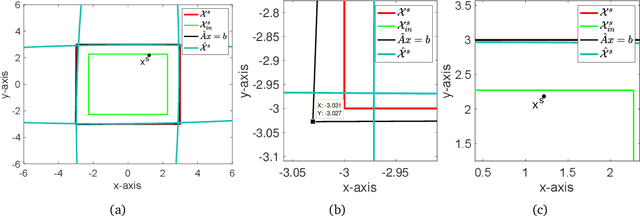
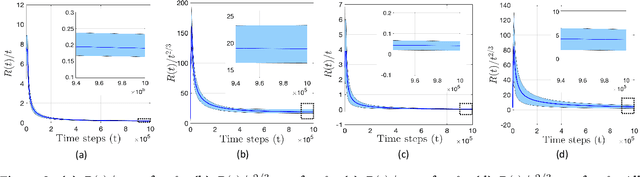
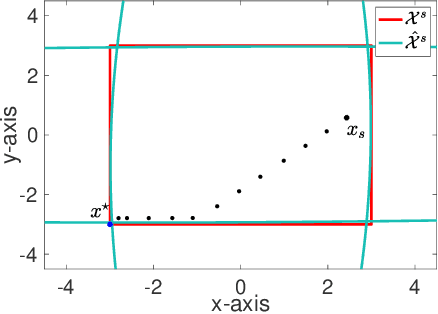
We study the problem of safe online convex optimization, where the action at each time step must satisfy a set of linear safety constraints. The goal is to select a sequence of actions to minimize the regret without violating the safety constraints at any time step (with high probability). The parameters that specify the linear safety constraints are unknown to the algorithm. The algorithm has access to only the noisy observations of constraints for the chosen actions. We propose an algorithm, called the {Safe Online Projected Gradient Descent} (SO-PGD) algorithm, to address this problem. We show that, under the assumption of the availability of a safe baseline action, the SO-PGD algorithm achieves a regret $O(T^{2/3})$. While there are many algorithms for online convex optimization (OCO) problems with safety constraints available in the literature, they allow constraint violations during learning/optimization, and the focus has been on characterizing the cumulative constraint violations. To the best of our knowledge, ours is the first work that provides an algorithm with provable guarantees on the regret, without violating the linear safety constraints (with high probability) at any time step.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge