Safe Exploration in Markov Decision Processes with Time-Variant Safety using Spatio-Temporal Gaussian Process
Paper and Code
Sep 12, 2018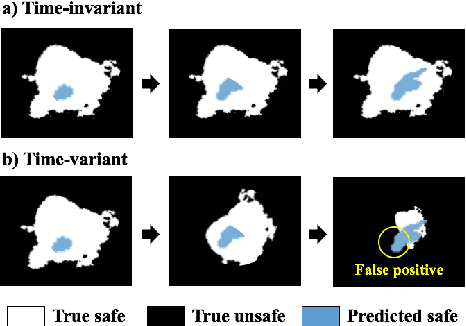

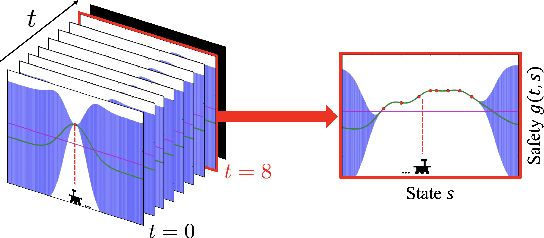

In many real-world applications (e.g., planetary exploration, robot navigation), an autonomous agent must be able to explore a space with guaranteed safety. Most safe exploration algorithms in the field of reinforcement learning and robotics have been based on the assumption that the safety features are a priori known and time-invariant. This paper presents a learning algorithm called ST-SafeMDP for exploring Markov decision processes (MDPs) that is based on the assumption that the safety features are a priori unknown and time-variant. In this setting, the agent explores MDPs while constraining the probability of entering unsafe states defined by a safety function being below a threshold. The unknown and time-variant safety values are modeled using a spatio-temporal Gaussian process. However, there remains an issue that an agent may have no viable action in a shrinking true safe space. To address this issue, we formulate a problem maximizing the cumulative number of safe states in the worst case scenario with respect to future observations. The effectiveness of this approach was demonstrated in two simulation settings, including one using real lunar terrain data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge