SADAM: Stochastic Adam, A Stochastic Operator for First-Order Gradient-based Optimizer
Paper and Code
May 20, 2022
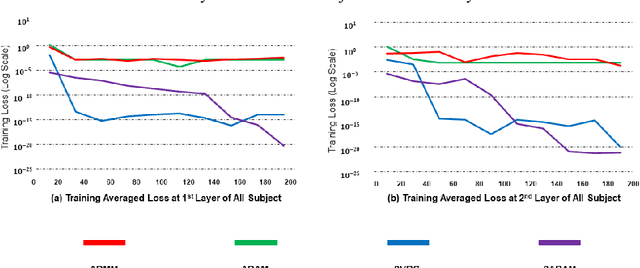

In this work, to efficiently help escape the stationary and saddle points, we propose, analyze, and generalize a stochastic strategy performed as an operator for a first-order gradient descent algorithm in order to increase the target accuracy and reduce time consumption. Unlike existing algorithms, the proposed stochastic the strategy does not require any batches and sampling techniques, enabling efficient implementation and maintaining the initial first-order optimizer's convergence rate, but provides an incomparable improvement of target accuracy when optimizing the target functions. In short, the proposed strategy is generalized, applied to Adam, and validated via the decomposition of biomedical signals using Deep Matrix Fitting and another four peer optimizers. The validation results show that the proposed random strategy can be easily generalized for first-order optimizers and efficiently improve the target accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge