RPN 2: On Interdependence Function Learning Towards Unifying and Advancing CNN, RNN, GNN, and Transformer

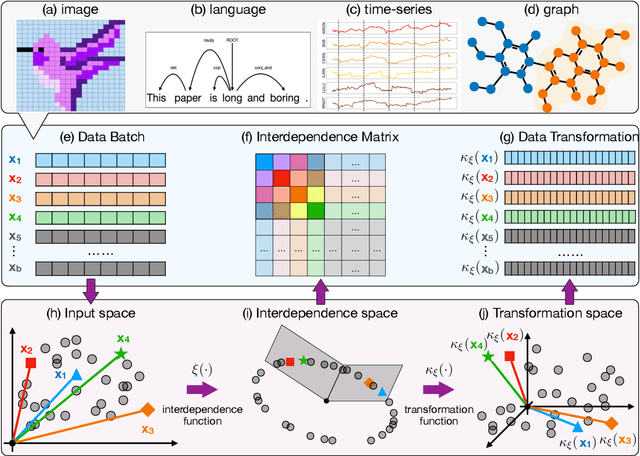
This paper builds upon our previous work on the Reconciled Polynomial Network (RPN). The original RPN model was designed under the assumption of input data independence, presuming the independence among both individual instances within data batches and attributes in each data instance. However, this assumption often proves invalid for function learning tasks involving complex, interdependent data such as language, images, time series, and graphs. Ignoring such data interdependence may inevitably lead to significant performance degradation. To overcome these limitations, we introduce the new Reconciled Polynomial Network (version 2), namely RPN 2, in this paper. By incorporating data and structural interdependence functions, RPN 2 explicitly models data interdependence via new component functions in its architecture. This enhancement not only significantly improves RPN 2's learning performance but also substantially expands its unifying potential, enabling it to encompass a broader range of contemporary dominant backbone models within its canonical representation. These backbones include, but are not limited to, convolutional neural networks (CNNs), recurrent neural networks (RNNs), graph neural networks (GNNs), and Transformers. Our analysis reveals that the fundamental distinctions among these backbone models primarily stem from their diverse approaches to defining the interdependence functions. Furthermore, this unified representation opens up new opportunities for designing innovative architectures with the potential to surpass the performance of these dominant backbones.