ROP inception: signal estimation with quadratic random sketching
Paper and Code
May 17, 2022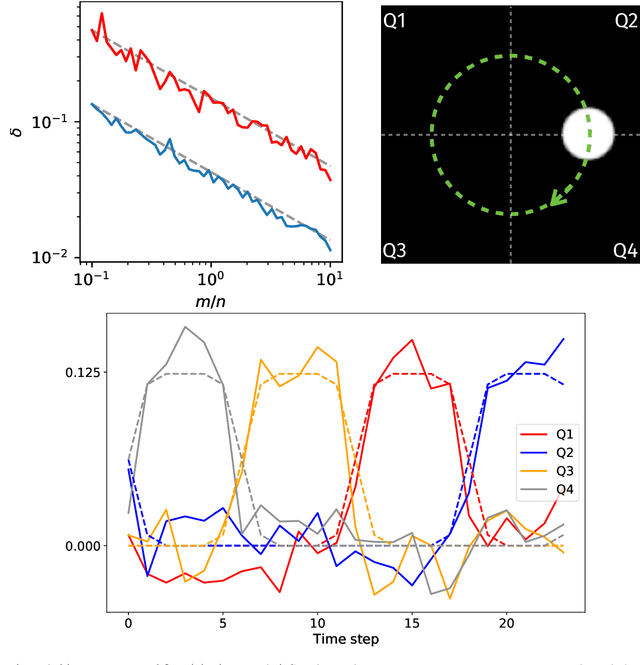
Rank-one projections (ROP) of matrices and quadratic random sketching of signals support several data processing and machine learning methods, as well as recent imaging applications, such as phase retrieval or optical processing units. In this paper, we demonstrate how signal estimation can be operated directly through such quadratic sketches--equivalent to the ROPs of the "lifted signal" obtained as its outer product with itself--without explicitly reconstructing that signal. Our analysis relies on showing that, up to a minor debiasing trick, the ROP measurement operator satisfies a generalised sign product embedding (SPE) property. In a nutshell, the SPE shows that the scalar product of a signal sketch with the "sign" of the sketch of a given pattern approximates the square of the projection of that signal on this pattern. This thus amounts to an insertion (an "inception") of a ROP model inside a ROP sketch. The effectiveness of our approach is evaluated in several synthetic experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge