Robust Tensor Recovery with Fiber Outliers for Traffic Events

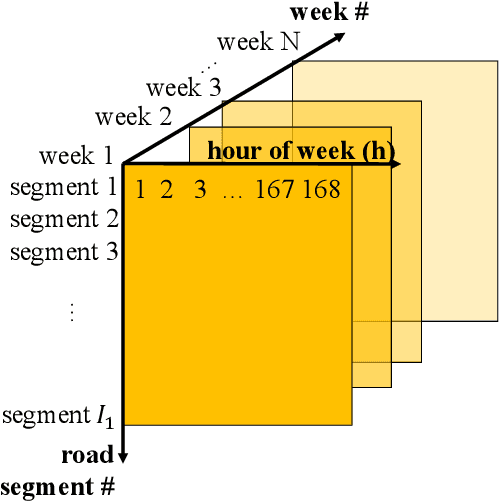
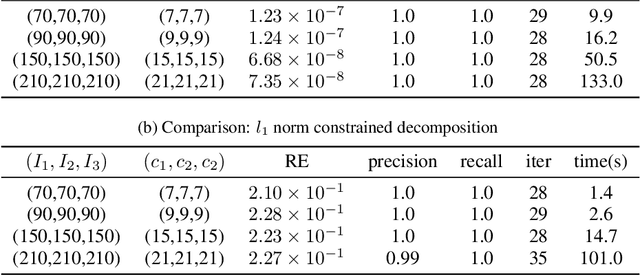
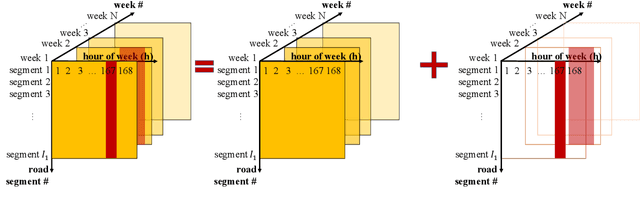
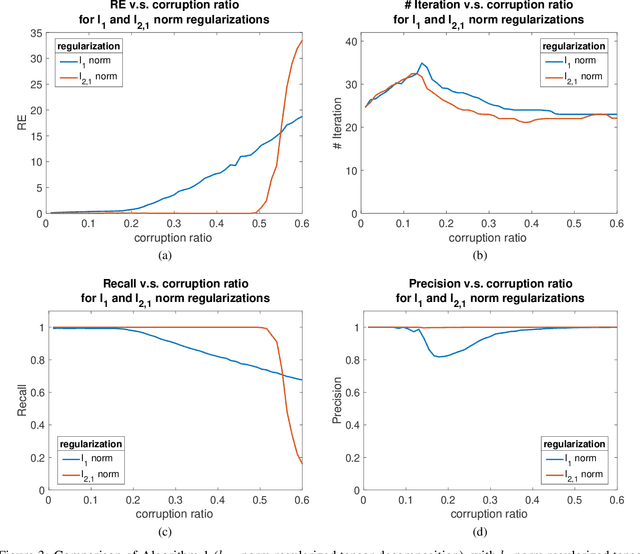
Event detection is gaining increasing attention in smart cities research. Large-scale mobility data serves as an important tool to uncover the dynamics of urban transportation systems, and more often than not the dataset is incomplete. In this article, we develop a method to detect extreme events in large traffic datasets, and to impute missing data during regular conditions. Specifically, we propose a robust tensor recovery problem to recover low rank tensors under fiber-sparse corruptions with partial observations, and use it to identify events, and impute missing data under typical conditions. Our approach is scalable to large urban areas, taking full advantage of the spatio-temporal correlations in traffic patterns. We develop an efficient algorithm to solve the tensor recovery problem based on the alternating direction method of multipliers (ADMM) framework. Compared with existing $l_1$ norm regularized tensor decomposition methods, our algorithm can exactly recover the values of uncorrupted fibers of a low rank tensor and find the positions of corrupted fibers under mild conditions. Numerical experiments illustrate that our algorithm can exactly detect outliers even with missing data rates as high as 40%, conditioned on the outlier corruption rate and the Tucker rank of the low rank tensor. Finally, we apply our method on a real traffic dataset corresponding to downtown Nashville, TN, USA and successfully detect the events like severe car crashes, construction lane closures, and other large events that cause significant traffic disruptions.