Robust Square Root Unscented Kalman filter of graph signals
Paper and Code
Sep 11, 2024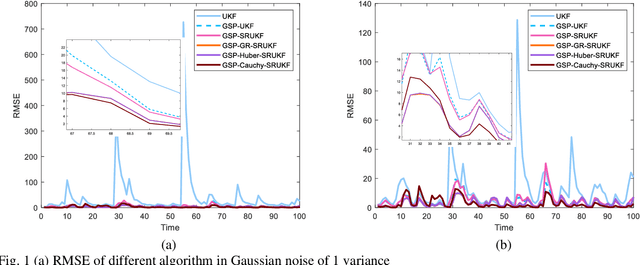
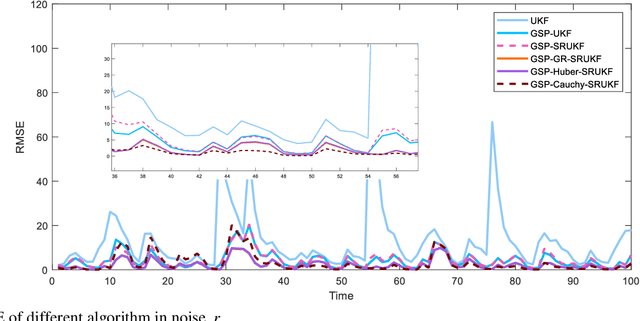
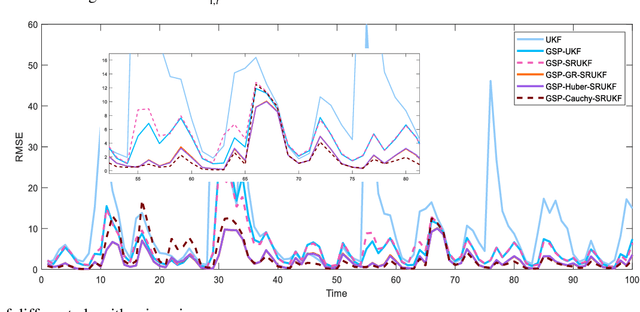
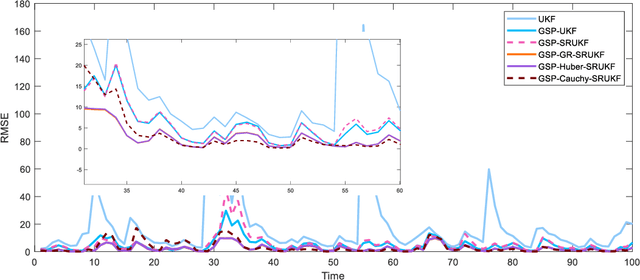
Considering the problem of nonlinear and non-gaussian filtering of the graph signal, in this paper, a robust square root unscented Kalman filter based on graph signal processing is proposed. The algorithm uses a graph topology to generate measurements and an unscented transformation is used to obtain the priori state estimates. In addition, in order to enhance the numerical stability of the unscented Kalman filter, the algorithm combines the double square root decomposition method to update the covariance matrix in the graph frequency domain. Furthermore, to handle the non-Gaussian noise problem in the state estimation process, an error augmentation model is constructed in the graph frequency domain by unifying the measurement error and state error, which utilizes the Laplace matrix of the graph to effectively reduce the cumulative error at each vertex. Then the general robust cost function is adopted as the optimal criterion to deal with the error, which has more parameter options so that effectively suppresses the problems of random outliers and abnormal measurement values in the state estimation process. Finally, the convergence of the error of the proposed algorithm is firstly verified theoretically, and then the robustness of the proposed algorithm is verified by experimental simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge