Robust Similarity and Distance Learning via Decision Forests
Paper and Code
Aug 21, 2020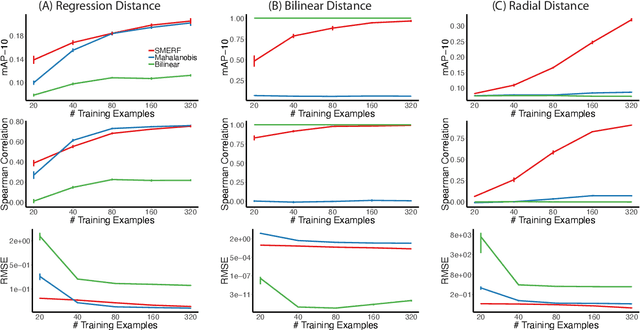
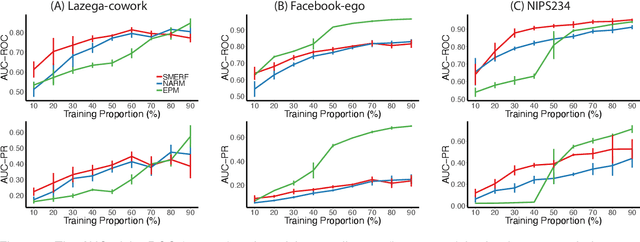
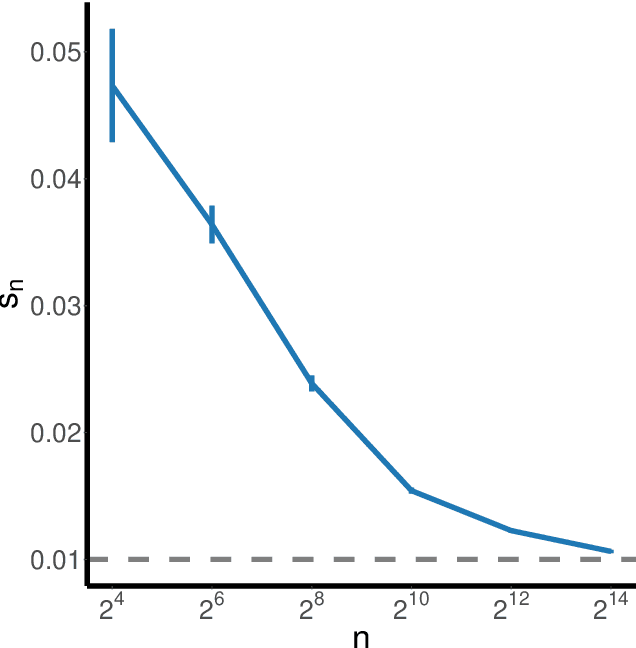
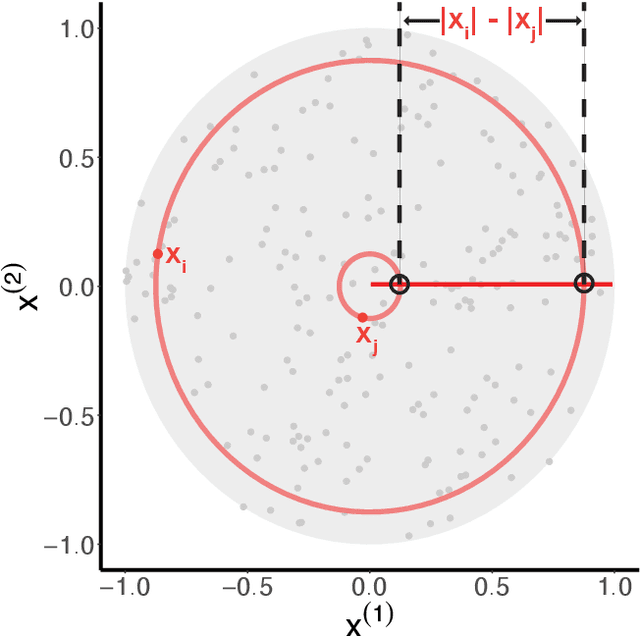
Canonical distances such as Euclidean distance often fail to capture the appropriate relationships between items, subsequently leading to subpar inference and prediction. Many algorithms have been proposed for automated learning of suitable distances, most of which employ linear methods to learn a global metric over the feature space. While such methods offer nice theoretical properties, interpretability, and computationally efficient means for implementing them, they are limited in expressive capacity. Methods which have been designed to improve expressiveness sacrifice one or more of the nice properties of the linear methods. To bridge this gap, we propose a highly expressive novel decision forest algorithm for the task of distance learning, which we call Similarity and Metric Random Forests (SMERF). We show that the tree construction procedure in SMERF is a proper generalization of standard classification and regression trees. Thus, the mathematical driving forces of SMERF are examined via its direct connection to regression forests, for which theory has been developed. Its ability to approximate arbitrary distances and identify important features is empirically demonstrated on simulated data sets. Last, we demonstrate that it accurately predicts links in networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge