Robust Semi-Supervised Classification for Multi-Relational Graphs
Paper and Code
Oct 19, 2015

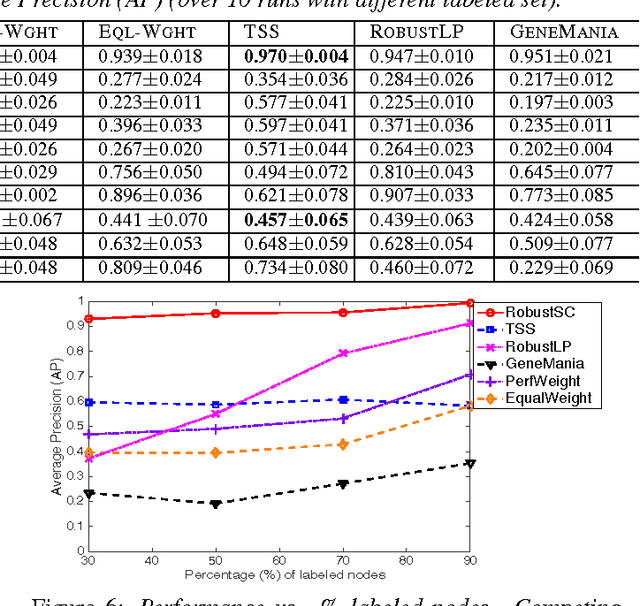
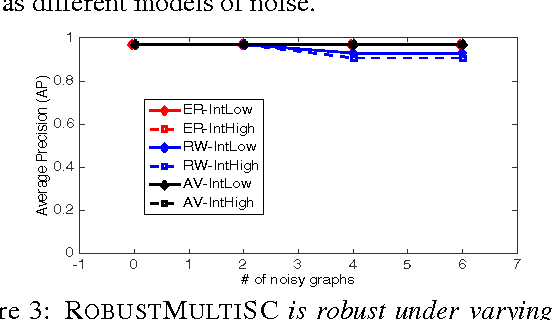
Graph-regularized semi-supervised learning has been used effectively for classification when (i) instances are connected through a graph, and (ii) labeled data is scarce. If available, using multiple relations (or graphs) between the instances can improve the prediction performance. On the other hand, when these relations have varying levels of veracity and exhibit varying relevance for the task, very noisy and/or irrelevant relations may deteriorate the performance. As a result, an effective weighing scheme needs to be put in place. In this work, we propose a robust and scalable approach for multi-relational graph-regularized semi-supervised classification. Under a convex optimization scheme, we simultaneously infer weights for the multiple graphs as well as a solution. We provide a careful analysis of the inferred weights, based on which we devise an algorithm that filters out irrelevant and noisy graphs and produces weights proportional to the informativeness of the remaining graphs. Moreover, the proposed method is linearly scalable w.r.t. the number of edges in the union of the multiple graphs. Through extensive experiments we show that our method yields superior results under different noise models, and under increasing number of noisy graphs and intensity of noise, as compared to a list of baselines and state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge