Robust Kalman filters with unknown covariance of multiplicative noise

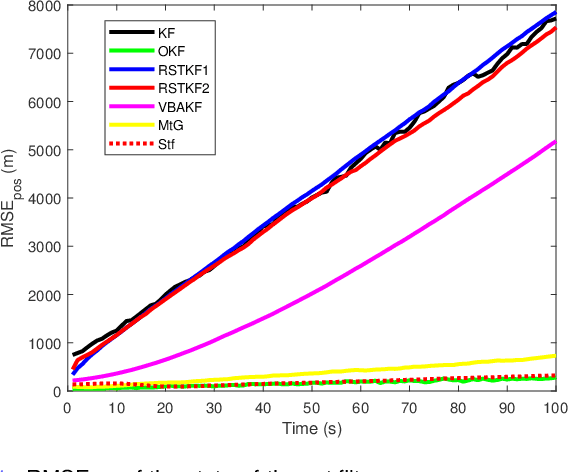
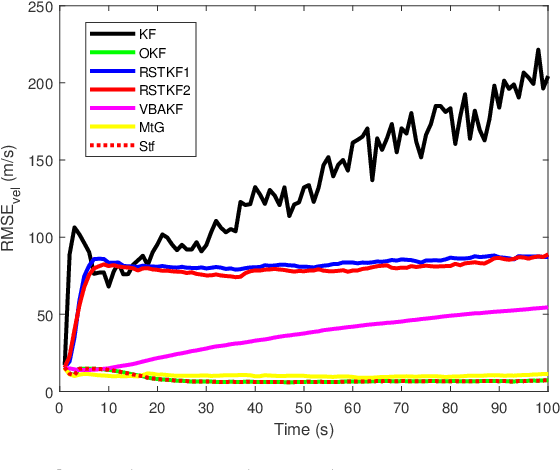
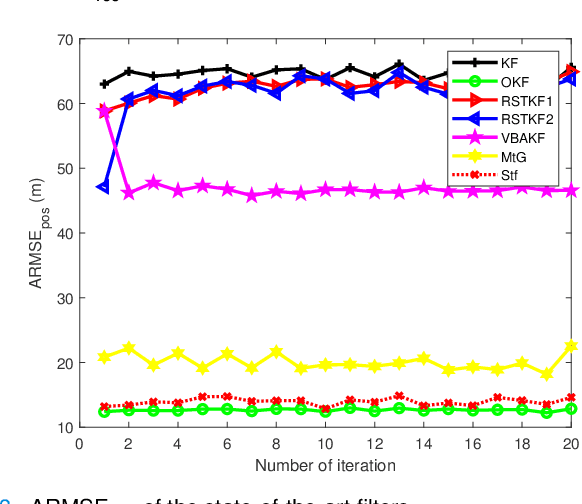
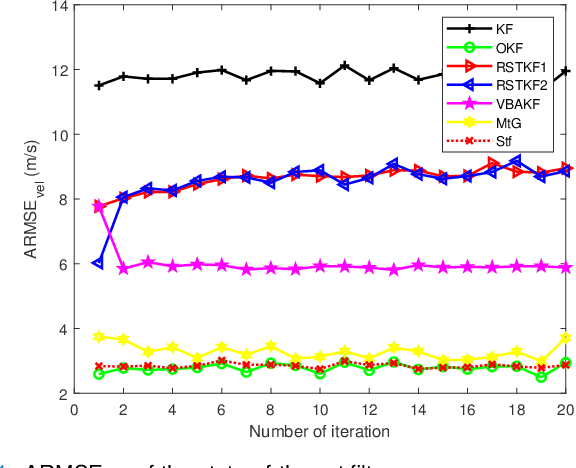
In this paper, state and noise covariance estimation problems for linear system with unknown multiplicative noise are considered. The measurement likelihood is modelled as a mixture of two Gaussian distributions and a Student's $\emph{t}$ distribution, respectively. The unknown covariance of multiplicative noise is modelled as an inverse Gamma/Wishart distribution and the initial condition is formulated as the nominal covariance. By using robust design and choosing hierarchical priors, two variational Bayesian based robust Kalman filters are proposed. Stability and covergence of the proposed filters, the covariance parameters, the VB inference, and the estimation error dynamics are analyzed. The lower and upper bounds are also provided to guarantee the performance of the proposed filters. A target tracking simulation is provided to validate the effectiveness of the proposed filters.