Robust, fast and accurate mapping of diffusional mean kurtosis
Paper and Code
Nov 30, 2022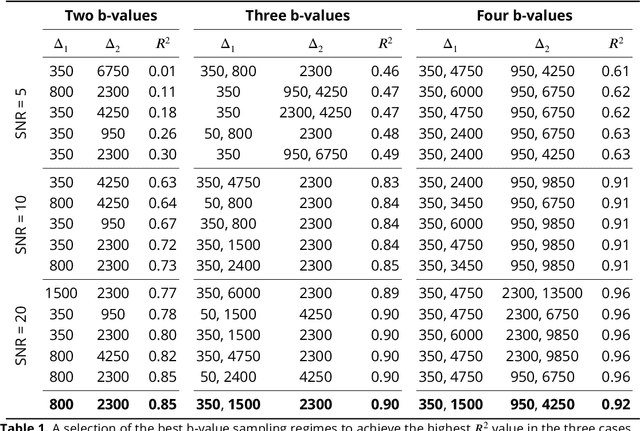
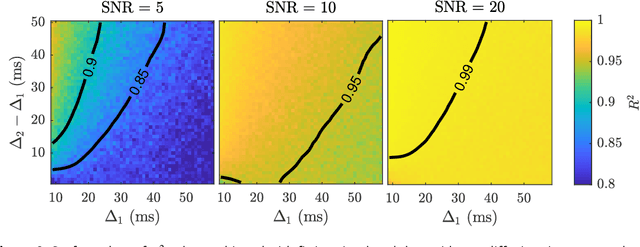
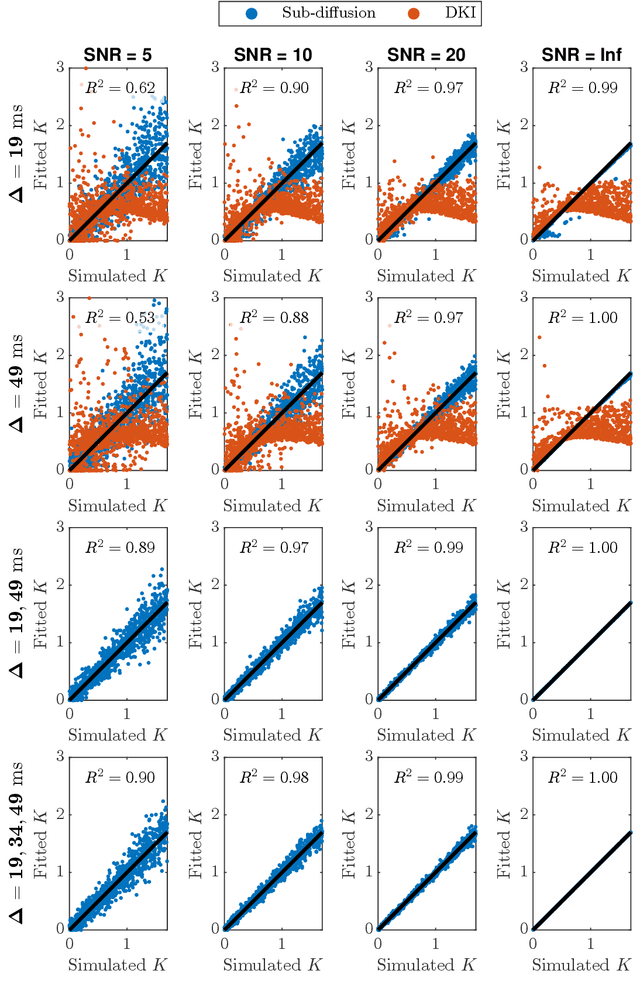
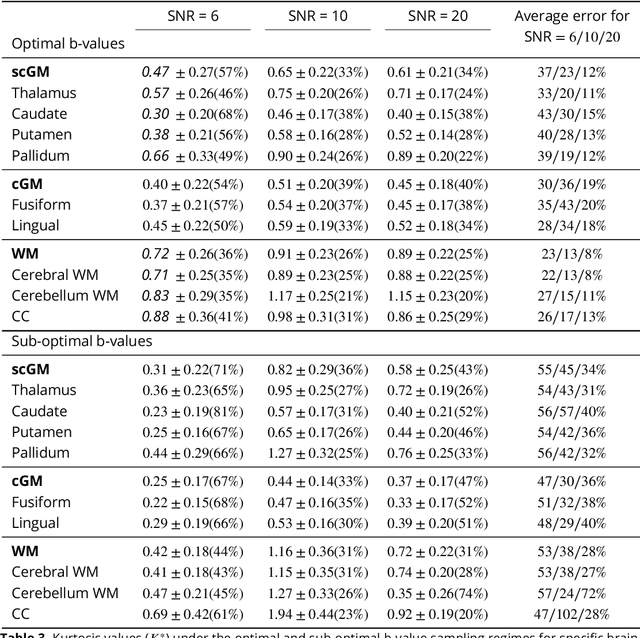
Diffusion weighted magnetic resonance imaging produces data encoded with the random motion of water molecules in biological tissues. The collection and extraction of information from such data have become critical to modern imaging studies, and particularly those focusing on neuroimaging. A range of mathematical models are routinely applied to infer tissue microstructure properties. Diffusional kurtosis imaging entails a model for measuring the extent of non-Gaussian diffusion in biological tissues. The method has seen wide assimilation across a range of clinical applications, and promises to be an increasingly important tool for clinical diagnosis, treatment planning and monitoring. However, accurate and robust estimation of kurtosis from clinically feasible data acquisitions remains a challenge. We outline a fast and robust way of estimating mean kurtosis via the sub-diffusion mathematical framework. Our kurtosis mapping method is evaluated using simulations and the Connectome 1.0 human brain data. Results show that fitting the sub-diffusion model to multiple diffusion time data and then directly calculating the mean kurtosis greatly improves the quality of the estimation. Suggestions for diffusion encoding sampling, the number of diffusion times to be acquired and the separation between them are provided. Exquisite tissue contrast is achieved even when the diffusion encoded data is collected in only minutes. Our findings suggest robust estimation of mean kurtosis can be realised within a clinically feasible diffusion weighted magnetic resonance imaging data acquisition time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge