Robot Monitoring for the Detection and Confirmation of Stochastic Events
Paper and Code
Sep 16, 2014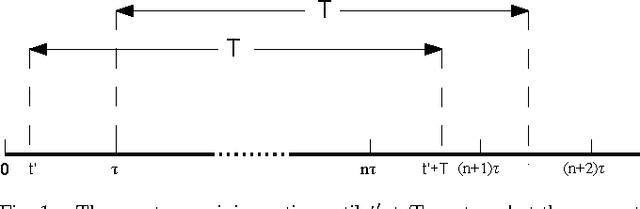
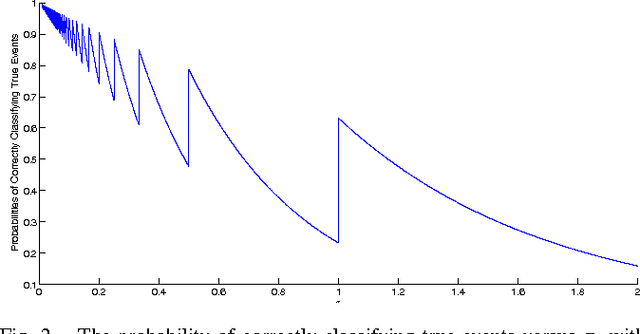
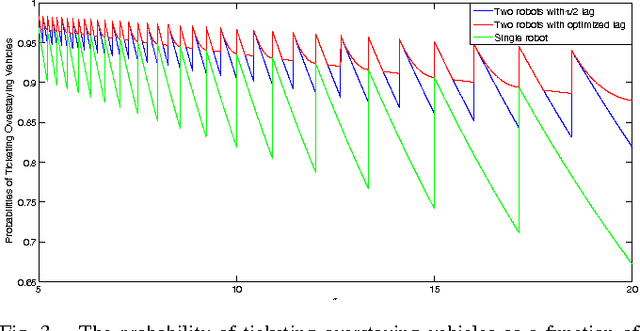
In this paper we consider a robot patrolling problem in which events arrive randomly over time at the vertices of a graph. When an event arrives it remains active for a random amount of time. If that time active exceeds a certain threshold, then we say that the event is a true event; otherwise it is a false event. The robot(s) can traverse the graph to detect newly arrived events, and can revisit these events in order to classify them as true or false. The goal is to plan robot paths that maximize the number of events that are correctly classified, with the constraint that there are no false positives. We show that the offline version of this problem is NP-hard. We then consider a simple patrolling policy based on the traveling salesman tour, and characterize the probability of correctly classifying an event. We investigate the problem when multiple robots follow the same path, and we derive the optimal (and not necessarily uniform) spacing between robots on the path.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge