Reward Biased Maximum Likelihood Estimation for Reinforcement Learning

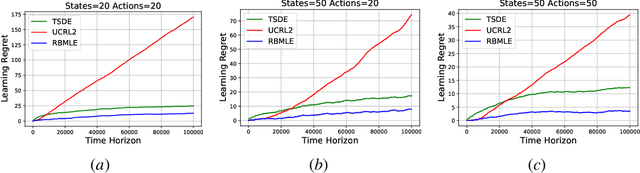
The Reward-Biased Maximum Likelihood Estimate (RBMLE) for adaptive control of Markov chains was proposed in (Kumar and Becker, 1982) to overcome the central obstacle of what is called the "closed-identifiability problem" of adaptive control, the "dual control problem" by Feldbaum (Feldbaum, 1960a,b), or the "exploration vs. exploitation problem". It exploited the key observation that since the maximum likelihood parameter estimator can asymptotically identify the closed-transition probabilities under a certainty equivalent approach (Borkar and Varaiya, 1979), the limiting parameter estimates must necessarily have an optimal reward that is less than the optimal reward for the true but unknown system. Hence it proposed a bias in favor of parameters with larger optimal rewards, providing a carefully structured solution to above problem. It thereby proposed an optimistic approach of favoring parameters with larger optimal rewards, now known as "optimism in the face of uncertainty." The RBMLE approach has been proved to be longterm average reward optimal in a variety of contexts including controlled Markov chains, linear quadratic Gaussian systems, some nonlinear systems, and diffusions. However, modern attention is focused on the much finer notion of "regret," or finite-time performance for all time, espoused by (Lai and Robbins, 1985). Recent analysis of RBMLE for multi-armed stochastic bandits (Liu et al., 2020) and linear contextual bandits (Hung et al., 2020) has shown that it has state-of-the-art regret and exhibits empirical performance comparable to or better than the best current contenders. Motivated by this, we examine the finite-time performance of RBMLE for reinforcement learning tasks of optimal control of unknown Markov Decision Processes. We show that it has a regret of $O(\log T)$ after $T$ steps, similar to state-of-art algorithms.