Revisiting visual-inertial structure from motion for odometry and SLAM initialization

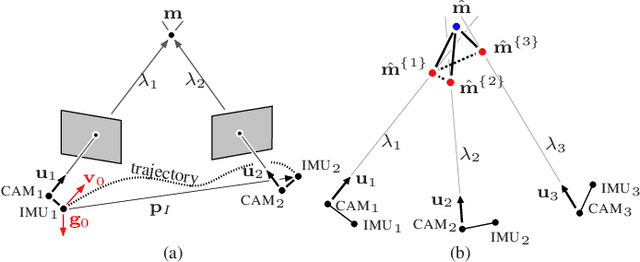
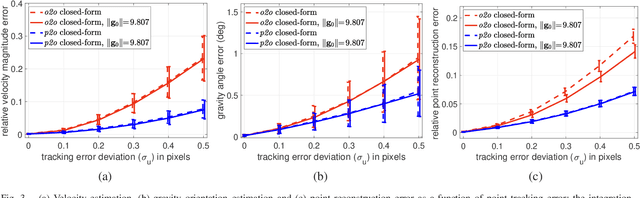
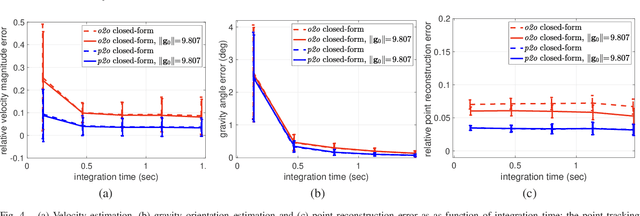
In this paper, an efficient closed-form solution for the state initialization in visual-inertial odometry (VIO) and simultaneous localization and mapping (SLAM) is presented. Unlike the state-of-the-art, we do not derive linear equations from triangulating pairs of point observations. Instead, we build on a direct triangulation of the unknown $3D$ point paired with each of its observations. We show and validate the high impact of such a simple difference. The resulting linear system has a simpler structure and the solution through analytic elimination only requires solving a $6\times 6$ linear system (or $9 \times 9$ when accelerometer bias is included). In addition, all the observations of every scene point are jointly related, thereby leading to a less biased and more robust solution. The proposed formulation attains up to $50$ percent decreased velocity and point reconstruction error compared to the standard closed-form solver. Apart from the inherent efficiency, fewer iterations are needed by any further non-linear refinement thanks to better parameter initialization. In this context, we provide the analytic Jacobians for a non-linear optimizer that optionally refines the initial parameters. The superior performance of the proposed solver is established by quantitative comparisons with the state-of-the-art solver.