Revisiting the Softmax Bellman Operator: Theoretical Properties and Practical Benefits

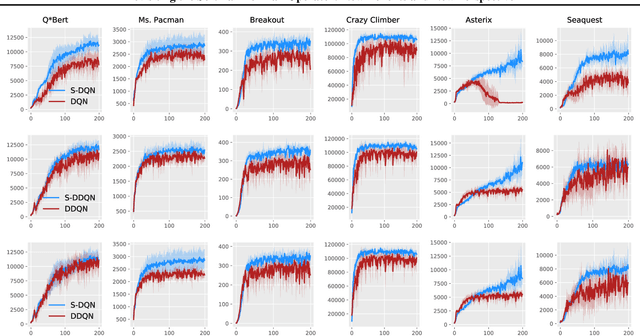
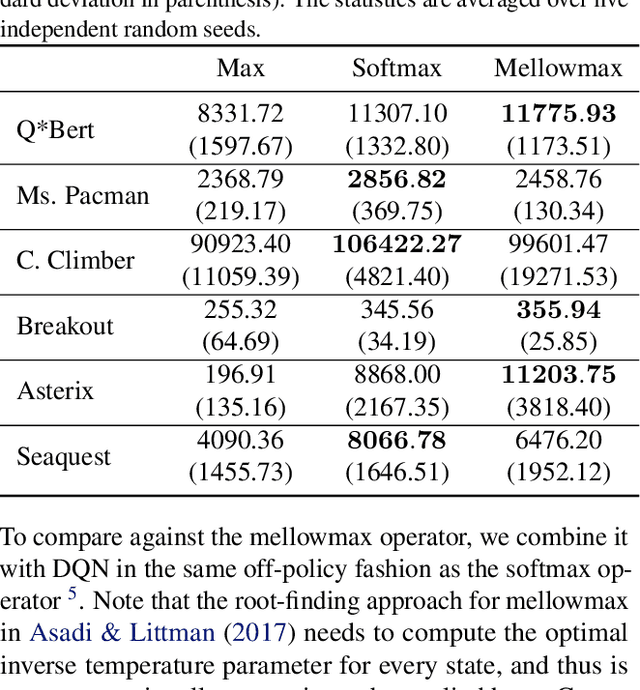
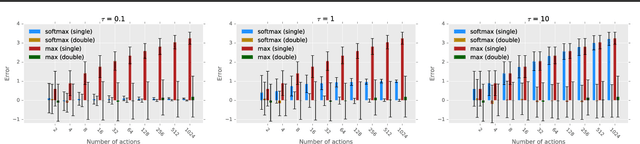
The softmax function has been primarily employed in reinforcement learning (RL) to improve exploration and provide a differentiable approximation to the max function, as also observed in the mellowmax paper by Asadi and Littman. This paper instead focuses on using the softmax function in the Bellman updates, independent of the exploration strategy. Our main theory provides a performance bound for the softmax Bellman operator, and shows it converges to the standard Bellman operator exponentially fast in the inverse temperature parameter. We also prove that under certain conditions, the softmax operator can reduce the overestimation error and the gradient noise. A detailed comparison among different Bellman operators is then presented to show the trade-off when selecting them. We apply the softmax operator to deep RL by combining it with the deep Q-network (DQN) and double DQN algorithms in an off-policy fashion, and demonstrate that these variants can often achieve better performance in several Atari games, and compare favorably to their mellowmax counterpart.