Revisiting Pooling through the Lens of Optimal Transport

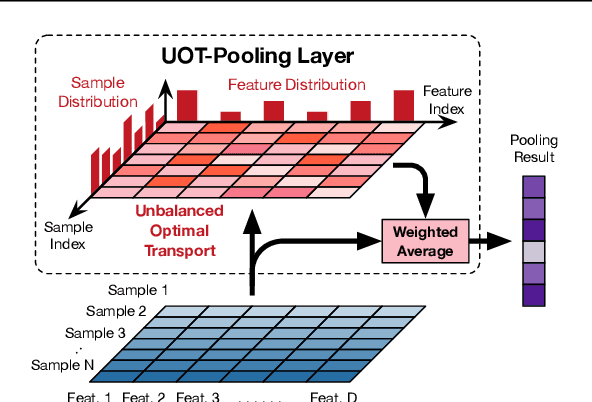
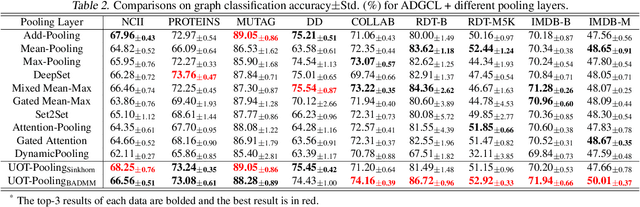
Pooling is one of the most significant operations in many machine learning models and tasks, whose implementation, however, is often empirical in practice. In this paper, we develop a novel and solid algorithmic pooling framework through the lens of optimal transport. In particular, we demonstrate that most existing pooling methods are equivalent to solving some specializations of an unbalanced optimal transport (UOT) problem. Making the parameters of the UOT problem learnable, we unify most existing pooling methods in the same framework, and accordingly, propose a generalized pooling layer called \textit{UOT-Pooling} for neural networks. Moreover, we implement the UOT-Pooling with two different architectures, based on the Sinkhorn scaling algorithm and the Bregman ADMM algorithm, respectively, and study their stability and efficiency quantitatively. We test our UOT-Pooling layers in two application scenarios, including multi-instance learning (MIL) and graph embedding. For state-of-the-art models of these two tasks, we can improve their performance by replacing conventional pooling layers with our UOT-Pooling layers.