Rethinking Estimation Rate for Wireless Sensing: A Rate-Distortion Perspective
Paper and Code
Mar 21, 2023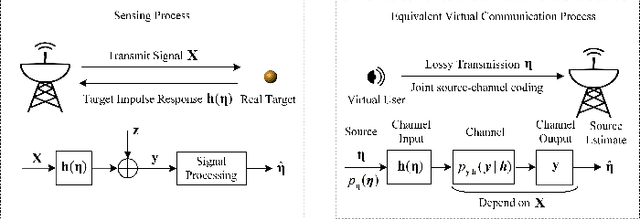
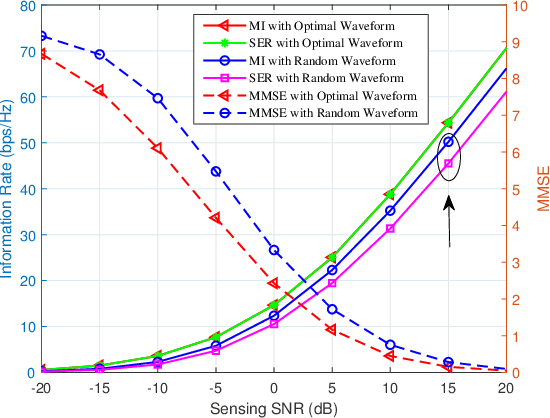
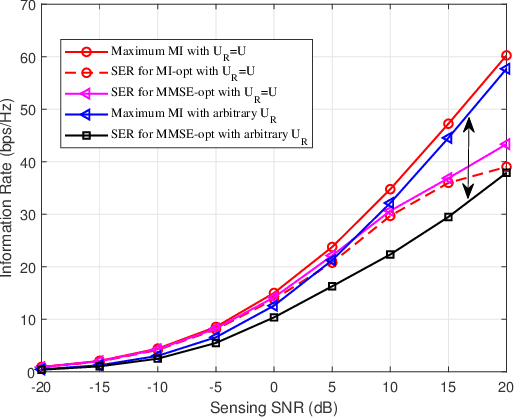
Wireless sensing has been recognized as a key enabling technology for numerous emerging applications. For decades, the sensing performance was mostly evaluated from a reliability perspective, with the efficiency aspect widely unexplored. Motivated from both backgrounds of rate-distortion theory and optimal sensing waveform design, a novel efficiency metric, namely, the sensing estimation rate (SER), is defined to unify the information- and estimation- theoretic perspectives of wireless sensing. Specifically, the active sensing process is characterized as a virtual lossy data transmission through non-cooperative joint source-channel coding. The bounds of SER are analyzed based on the data processing inequality, followed by a detailed derivation of achievable bounds under the special cases of the Gaussian linear model (GLM) and semi-controllable GLM. As for the intractable non-linear model, a computable upper bound is also given in terms of the Bayesian Cram\'er-Rao bound (BCRB). Finally, we show the rationality and effectiveness of the SER defined by comparing to the related works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge