Resilient Consensus-based Multi-agent Reinforcement Learning with Function Approximation
Paper and Code
Nov 18, 2021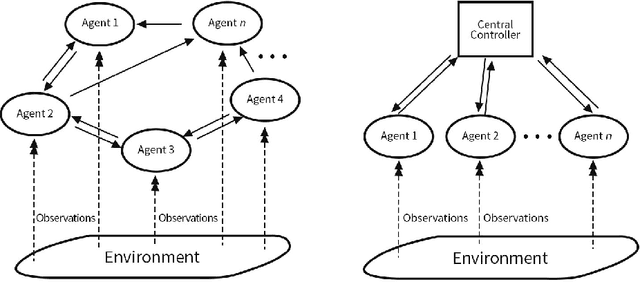
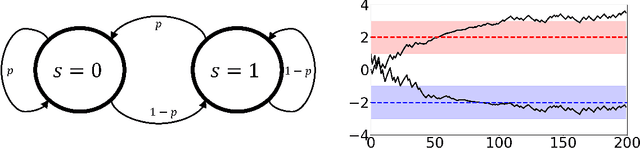
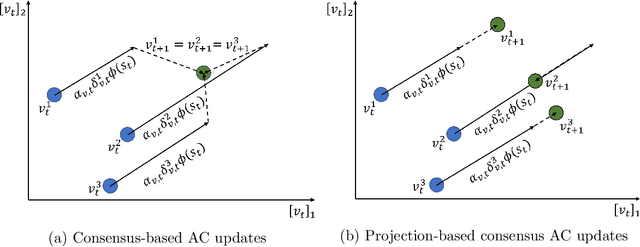
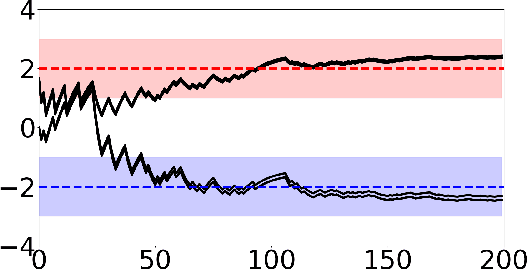
Adversarial attacks during training can strongly influence the performance of multi-agent reinforcement learning algorithms. It is, thus, highly desirable to augment existing algorithms such that the impact of adversarial attacks on cooperative networks is eliminated, or at least bounded. In this work, we consider a fully decentralized network, where each agent receives a local reward and observes the global state and action. We propose a resilient consensus-based actor-critic algorithm, whereby each agent estimates the team-average reward and value function, and communicates the associated parameter vectors to its immediate neighbors. We show that in the presence of Byzantine agents, whose estimation and communication strategies are completely arbitrary, the estimates of the cooperative agents converge to a bounded consensus value with probability one, provided that there are at most $H$ Byzantine agents in the neighborhood of each cooperative agent and the network is $(2H+1)$-robust. Furthermore, we prove that the policy of the cooperative agents converges with probability one to a bounded neighborhood around a local maximizer of their team-average objective function under the assumption that the policies of the adversarial agents asymptotically become stationary.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge