Relation Embedding with Dihedral Group in Knowledge Graph
Paper and Code
Jun 03, 2019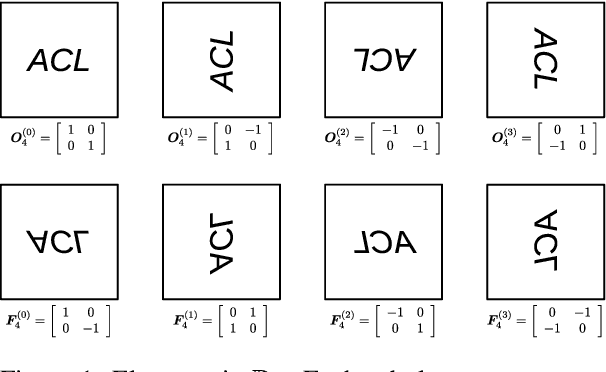

Link prediction is critical for the application of incomplete knowledge graph (KG) in the downstream tasks. As a family of effective approaches for link predictions, embedding methods try to learn low-rank representations for both entities and relations such that the bilinear form defined therein is a well-behaved scoring function. Despite of their successful performances, existing bilinear forms overlook the modeling of relation compositions, resulting in lacks of interpretability for reasoning on KG. To fulfill this gap, we propose a new model called DihEdral, named after dihedral symmetry group. This new model learns knowledge graph embeddings that can capture relation compositions by nature. Furthermore, our approach models the relation embeddings parametrized by discrete values, thereby decrease the solution space drastically. Our experiments show that DihEdral is able to capture all desired properties such as (skew-) symmetry, inversion and (non-) Abelian composition, and outperforms existing bilinear form based approach and is comparable to or better than deep learning models such as ConvE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge