Reinforcement Learning with Exogenous States and Rewards
Paper and Code
Mar 22, 2023
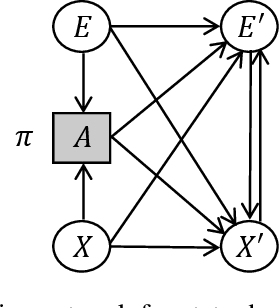
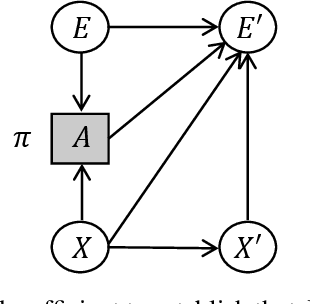
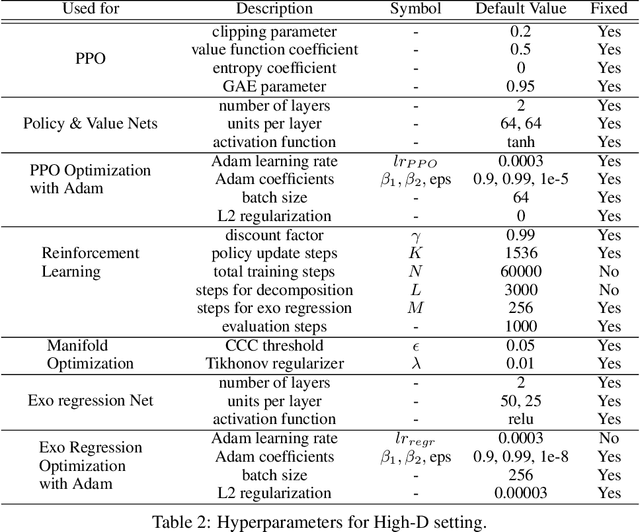
Exogenous state variables and rewards can slow reinforcement learning by injecting uncontrolled variation into the reward signal. This paper formalizes exogenous state variables and rewards and shows that if the reward function decomposes additively into endogenous and exogenous components, the MDP can be decomposed into an exogenous Markov Reward Process (based on the exogenous reward) and an endogenous Markov Decision Process (optimizing the endogenous reward). Any optimal policy for the endogenous MDP is also an optimal policy for the original MDP, but because the endogenous reward typically has reduced variance, the endogenous MDP is easier to solve. We study settings where the decomposition of the state space into exogenous and endogenous state spaces is not given but must be discovered. The paper introduces and proves correctness of algorithms for discovering the exogenous and endogenous subspaces of the state space when they are mixed through linear combination. These algorithms can be applied during reinforcement learning to discover the exogenous space, remove the exogenous reward, and focus reinforcement learning on the endogenous MDP. Experiments on a variety of challenging synthetic MDPs show that these methods, applied online, discover large exogenous state spaces and produce substantial speedups in reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge