Reinforcement Learning reveals fundamental limits on the mixing of active particles

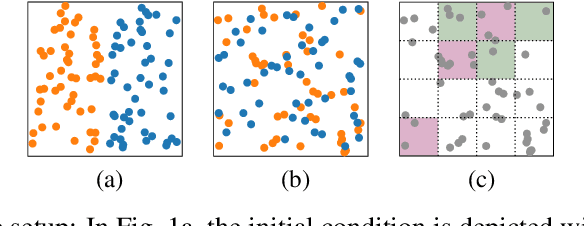
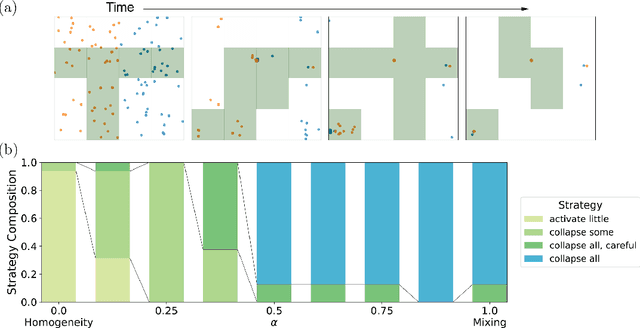
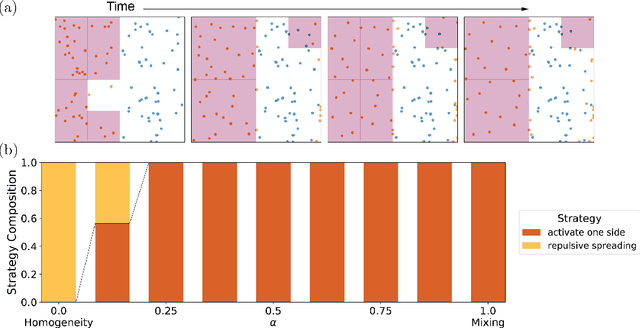
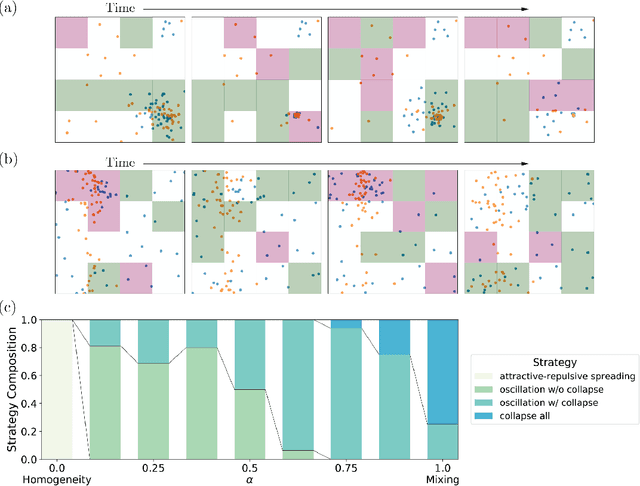
The control of far-from-equilibrium physical systems, including active materials, has emerged as an important area for the application of reinforcement learning (RL) strategies to derive control policies for physical systems. In active materials, non-linear dynamics and long-range interactions between particles prohibit closed-form descriptions of the system's dynamics and prevent explicit solutions to optimal control problems. Due to fundamental challenges in solving for explicit control strategies, RL has emerged as an approach to derive control strategies for far-from-equilibrium active matter systems. However, an important open question is how the mathematical structure and the physical properties of the active matter systems determine the tractability of RL for learning control policies. In this work, we show that RL can only find good strategies to the canonical active matter task of mixing for systems that combine attractive and repulsive particle interactions. Using mathematical results from dynamical systems theory, we relate the availability of both interaction types with the existence of hyperbolic dynamics and the ability of RL to find homogeneous mixing strategies. In particular, we show that for drag-dominated translational-invariant particle systems, hyperbolic dynamics and, therefore, mixing requires combining attractive and repulsive interactions. Broadly, our work demonstrates how fundamental physical and mathematical properties of dynamical systems can enable or constrain reinforcement learning-based control.