Reinforcement learning for linear-convex models with jumps via stability analysis of feedback controls
Paper and Code
Apr 19, 2021
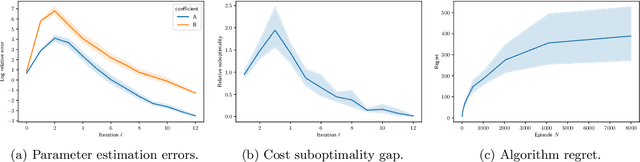
We study finite-time horizon continuous-time linear-convex reinforcement learning problems in an episodic setting. In this problem, the unknown linear jump-diffusion process is controlled subject to nonsmooth convex costs. We show that the associated linear-convex control problems admit Lipchitz continuous optimal feedback controls and further prove the Lipschitz stability of the feedback controls, i.e., the performance gap between applying feedback controls for an incorrect model and for the true model depends Lipschitz-continuously on the magnitude of perturbations in the model coefficients; the proof relies on a stability analysis of the associated forward-backward stochastic differential equation. We then propose a novel least-squares algorithm which achieves a regret of the order $O(\sqrt{N\ln N})$ on linear-convex learning problems with jumps, where $N$ is the number of learning episodes; the analysis leverages the Lipschitz stability of feedback controls and concentration properties of sub-Weibull random variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge