Reinforcement learning-assisted quantum architecture search for variational quantum algorithms
Paper and Code
Mar 07, 2024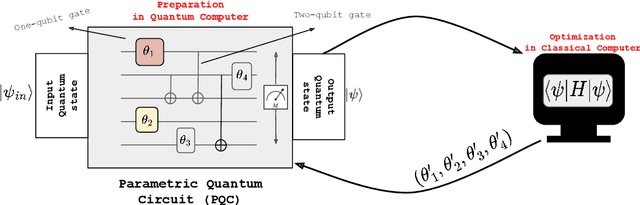
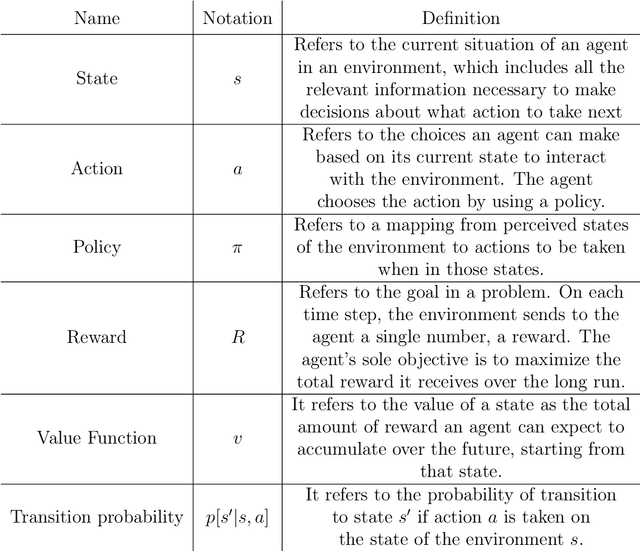
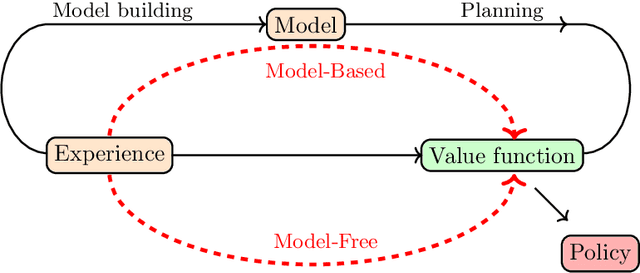
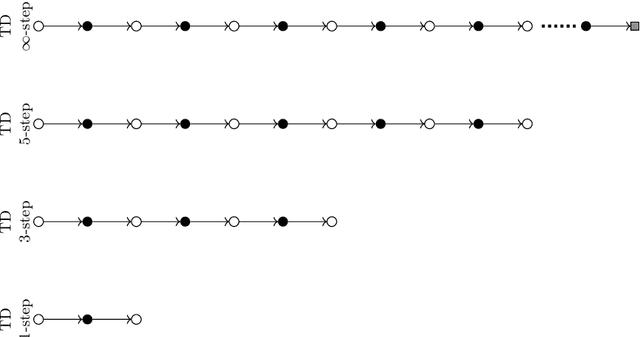
A significant hurdle in the noisy intermediate-scale quantum (NISQ) era is identifying functional quantum circuits. These circuits must also adhere to the constraints imposed by current quantum hardware limitations. Variational quantum algorithms (VQAs), a class of quantum-classical optimization algorithms, were developed to address these challenges in the currently available quantum devices. However, the overall performance of VQAs depends on the initialization strategy of the variational circuit, the structure of the circuit (also known as ansatz), and the configuration of the cost function. Focusing on the structure of the circuit, in this thesis, we improve the performance of VQAs by automating the search for an optimal structure for the variational circuits using reinforcement learning (RL). Within the thesis, the optimality of a circuit is determined by evaluating its depth, the overall count of gates and parameters, and its accuracy in solving the given problem. The task of automating the search for optimal quantum circuits is known as quantum architecture search (QAS). The majority of research in QAS is primarily focused on a noiseless scenario. Yet, the impact of noise on the QAS remains inadequately explored. In this thesis, we tackle the issue by introducing a tensor-based quantum circuit encoding, restrictions on environment dynamics to explore the search space of possible circuits efficiently, an episode halting scheme to steer the agent to find shorter circuits, a double deep Q-network (DDQN) with an $\epsilon$-greedy policy for better stability. The numerical experiments on noiseless and noisy quantum hardware show that in dealing with various VQAs, our RL-based QAS outperforms existing QAS. Meanwhile, the methods we propose in the thesis can be readily adapted to address a wide range of other VQAs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge