Regularized Wasserstein Means Based on Variational Transportation

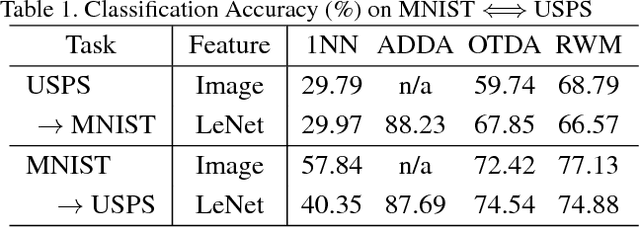
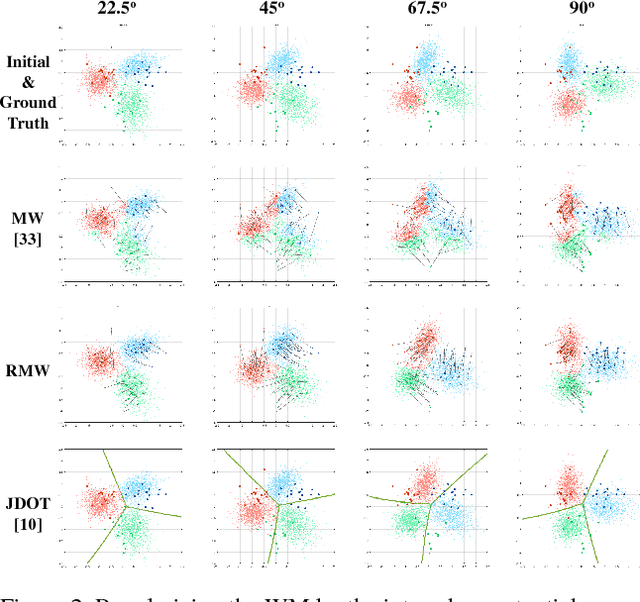
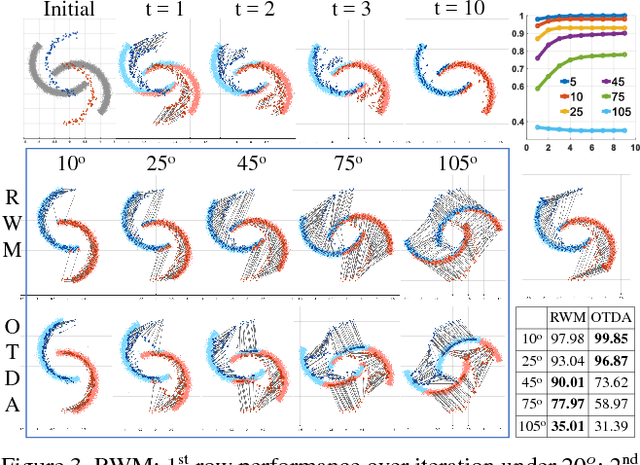
We raise the problem of regularizing Wasserstein means and propose several terms tailored to tackle different problems. Our formulation is based on variational transportation to distribute a sparse discrete measure into the target domain without mass splitting. The resulting sparse representation well captures the desired property of the domain while maintaining a small reconstruction error. We demonstrate the scalability and robustness of our method with examples of domain adaptation and skeleton layout.