Regularized Policies are Reward Robust

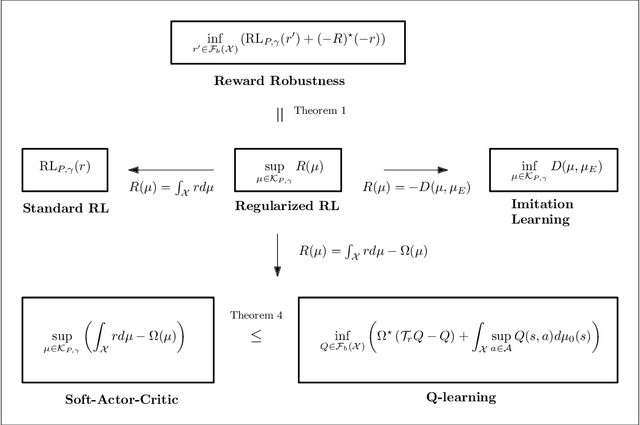
Entropic regularization of policies in Reinforcement Learning (RL) is a commonly used heuristic to ensure that the learned policy explores the state-space sufficiently before overfitting to a local optimal policy. The primary motivation for using entropy is for exploration and disambiguating optimal policies; however, the theoretical effects are not entirely understood. In this work, we study the more general regularized RL objective and using Fenchel duality; we derive the dual problem which takes the form of an adversarial reward problem. In particular, we find that the optimal policy found by a regularized objective is precisely an optimal policy of a reinforcement learning problem under a worst-case adversarial reward. Our result allows us to reinterpret the popular entropic regularization scheme as a form of robustification. Furthermore, due to the generality of our results, we apply to other existing regularization schemes. Our results thus give insights into the effects of regularization of policies and deepen our understanding of exploration through robust rewards at large.