Regularized Mutual Information Neural Estimation

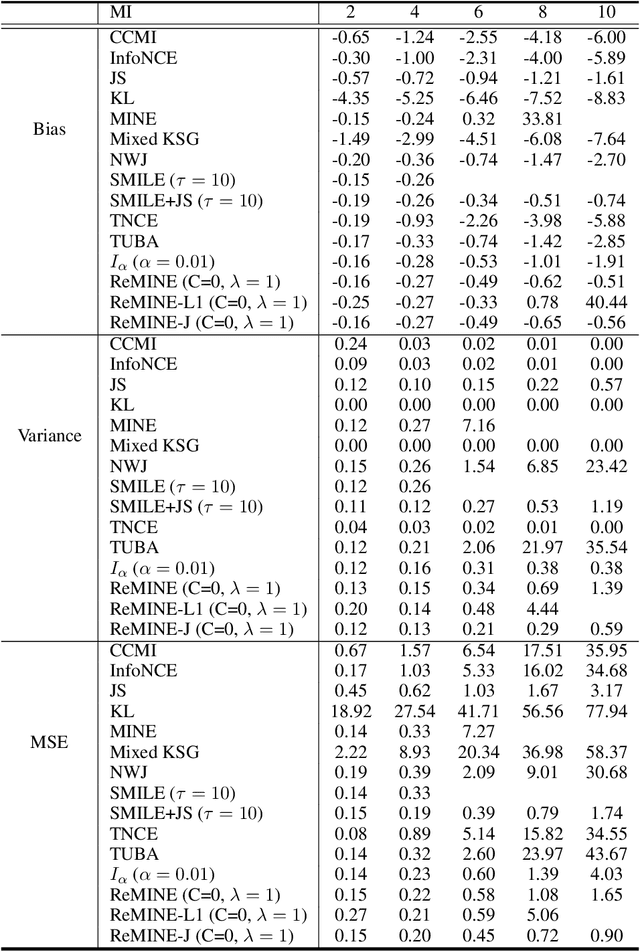
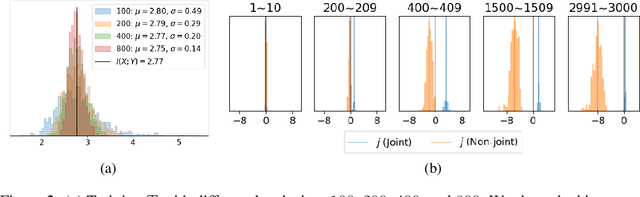
With the variational lower bound of mutual information (MI), the estimation of MI can be understood as an optimization task via stochastic gradient descent. In this work, we start by showing how Mutual Information Neural Estimator (MINE) searches for the optimal function $T$ that maximizes the Donsker-Varadhan representation. With our synthetic dataset, we directly observe the neural network outputs during the optimization to investigate why MINE succeeds or fails: We discover the drifting phenomenon, where the constant term of $T$ is shifting through the optimization process, and analyze the instability caused by the interaction between the $logsumexp$ and the insufficient batch size. Next, through theoretical and experimental evidence, we propose a novel lower bound that effectively regularizes the neural network to alleviate the problems of MINE. We also introduce an averaging strategy that produces an unbiased estimate by utilizing multiple batches to mitigate the batch size limitation. Finally, we show that $L^2$ regularization achieves significant improvements in both discrete and continuous settings.