Regret, stability, and fairness in matching markets with bandit learners
Paper and Code
Feb 11, 2021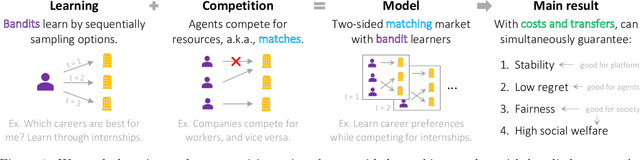
We consider the two-sided matching market with bandit learners. In the standard matching problem, users and providers are matched to ensure incentive compatibility via the notion of stability. However, contrary to the core assumption of the matching problem, users and providers do not know their true preferences a priori and must learn them. To address this assumption, recent works propose to blend the matching and multi-armed bandit problems. They establish that it is possible to assign matchings that are stable (i.e., incentive-compatible) at every time step while also allowing agents to learn enough so that the system converges to matchings that are stable under the agents' true preferences. However, while some agents may incur low regret under these matchings, others can incur high regret -- specifically, $\Omega(T)$ optimal regret where $T$ is the time horizon. In this work, we incorporate costs and transfers in the two-sided matching market with bandit learners in order to faithfully model competition between agents. We prove that, under our framework, it is possible to simultaneously guarantee four desiderata: (1) incentive compatibility, i.e., stability, (2) low regret, i.e., $O(\log(T))$ optimal regret, (3) fairness in the distribution of regret among agents, and (4) high social welfare.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge