Regression via Implicit Models and Optimal Transport Cost Minimization
Paper and Code
Mar 03, 2020
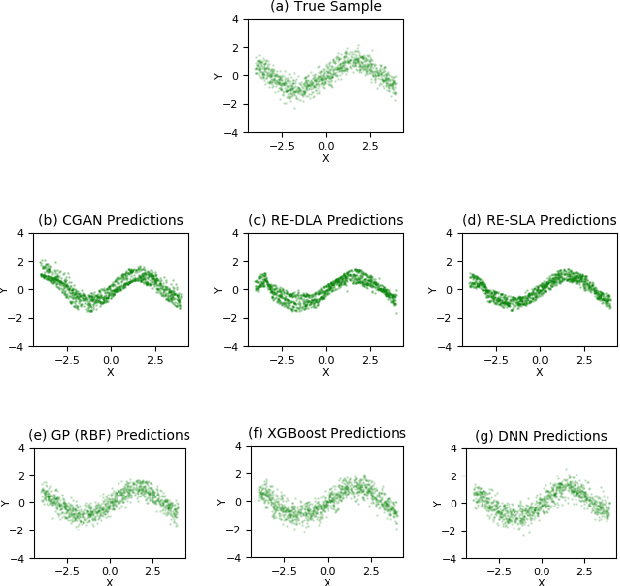
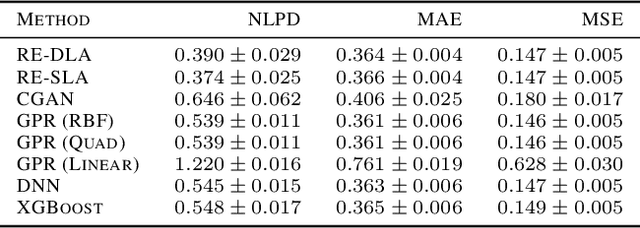
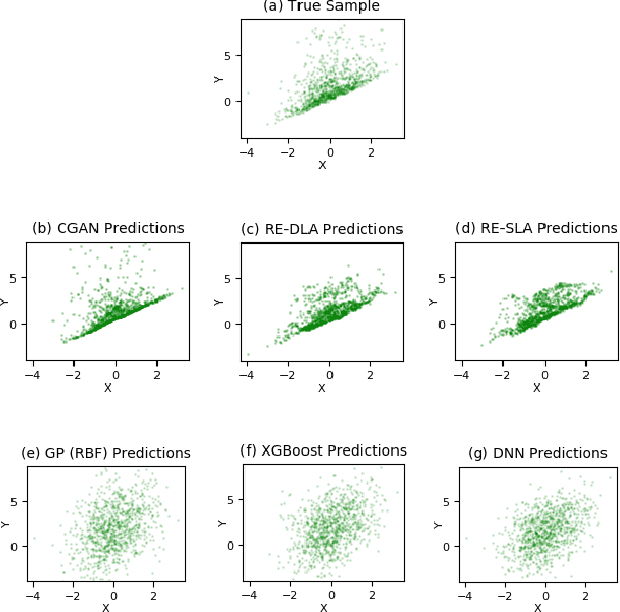
This paper addresses the classic problem of regression, which involves the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$. Recently, Conditional GAN (CGAN) has been applied for regression and has shown to be advantageous over the other standard approaches like Gaussian Process Regression, given its ability to implicitly model complex noise forms. However, the current CGAN implementation for regression uses the classical generator-discriminator architecture with the minimax optimization approach, which is notorious for being difficult to train due to issues like training instability or failure to converge. In this paper, we take another step towards regression models that implicitly model the noise, and propose a solution which directly optimizes the optimal transport cost between the true probability distribution $p(y|x)$ and the estimated distribution $\hat{p}(y|x)$ and does not suffer from the issues associated with the minimax approach. On a variety of synthetic and real-world datasets, our proposed solution achieves state-of-the-art results. The code accompanying this paper is available at "https://github.com/gurdaspuriya/ot_regression".
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge