Recurrent Highway Networks
Paper and Code
Jul 04, 2017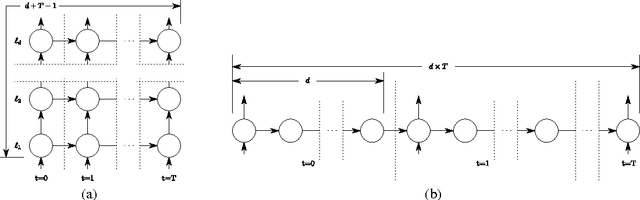
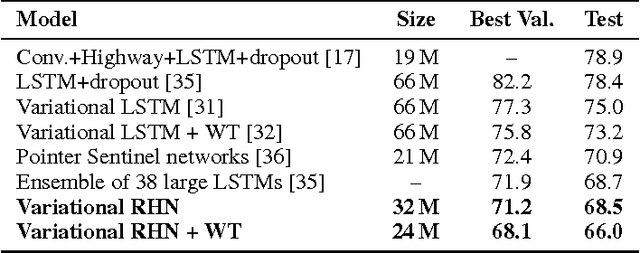
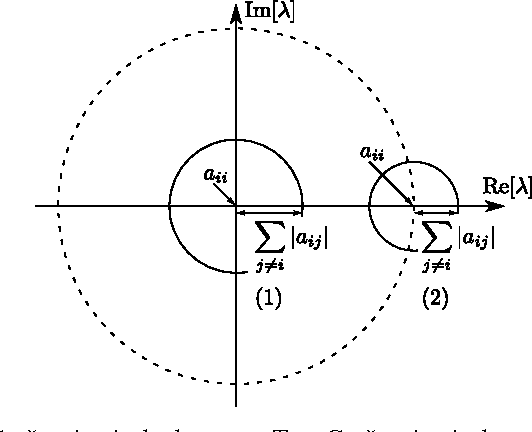
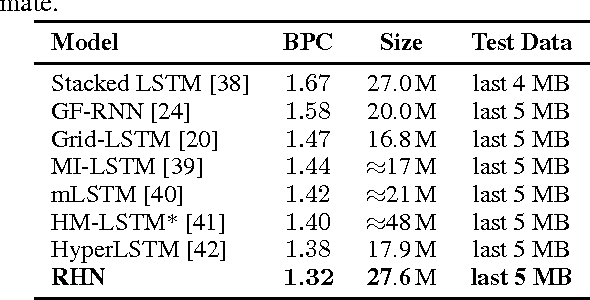
Many sequential processing tasks require complex nonlinear transition functions from one step to the next. However, recurrent neural networks with 'deep' transition functions remain difficult to train, even when using Long Short-Term Memory (LSTM) networks. We introduce a novel theoretical analysis of recurrent networks based on Gersgorin's circle theorem that illuminates several modeling and optimization issues and improves our understanding of the LSTM cell. Based on this analysis we propose Recurrent Highway Networks, which extend the LSTM architecture to allow step-to-step transition depths larger than one. Several language modeling experiments demonstrate that the proposed architecture results in powerful and efficient models. On the Penn Treebank corpus, solely increasing the transition depth from 1 to 10 improves word-level perplexity from 90.6 to 65.4 using the same number of parameters. On the larger Wikipedia datasets for character prediction (text8 and enwik8), RHNs outperform all previous results and achieve an entropy of 1.27 bits per character.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge