Real-valued Evolutionary Multi-modal Multi-objective Optimization by Hill-Valley Clustering
Paper and Code
Oct 28, 2020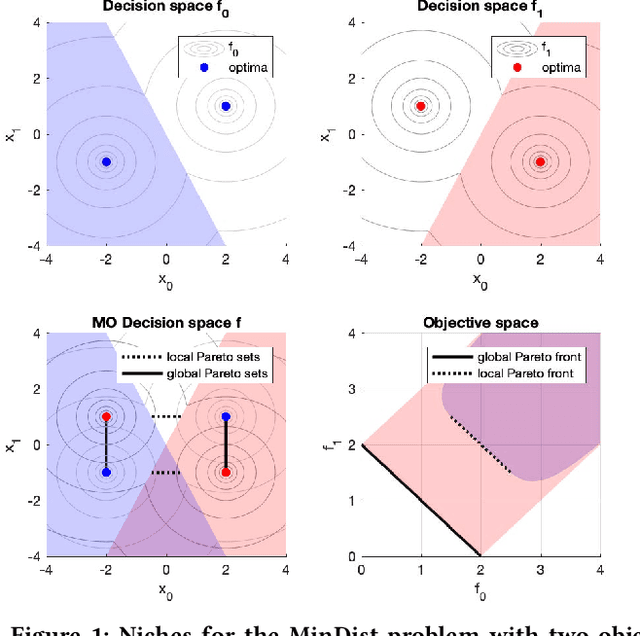
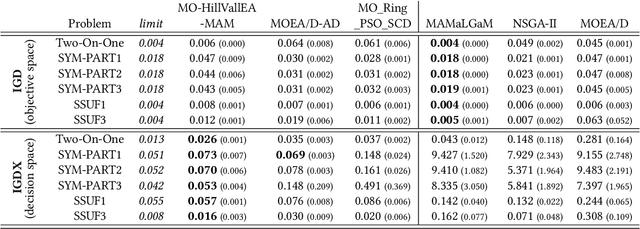

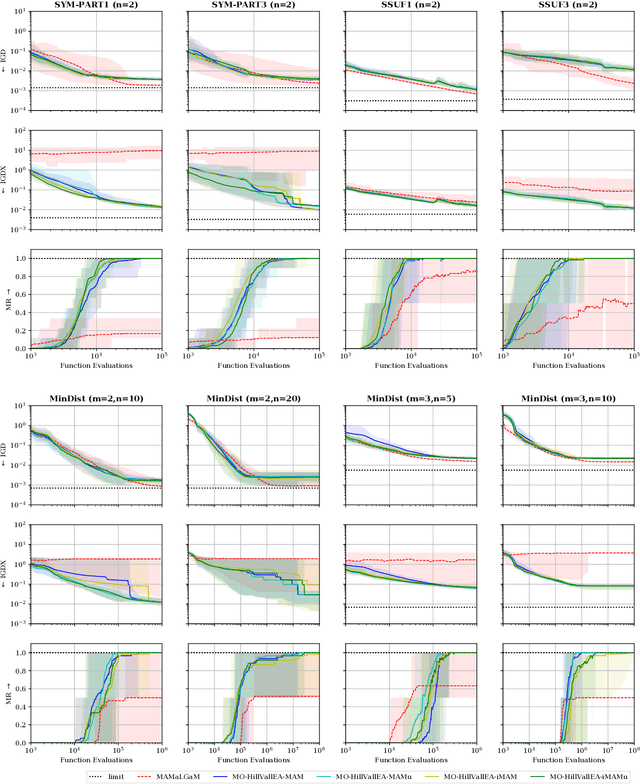
In model-based evolutionary algorithms (EAs), the underlying search distribution is adapted to the problem at hand, for example based on dependencies between decision variables. Hill-valley clustering is an adaptive niching method in which a set of solutions is clustered such that each cluster corresponds to a single mode in the fitness landscape. This can be used to adapt the search distribution of an EA to the number of modes, exploring each mode separately. Especially in a black-box setting, where the number of modes is a priori unknown, an adaptive approach is essential for good performance. In this work, we introduce multi-objective hill-valley clustering and combine it with MAMaLGaM, a multi-objective EA, into the multi-objective hill-valley EA (MO-HillVallEA). We empirically show that MO-HillVallEA outperforms MAMaLGaM and other well-known multi-objective optimization algorithms on a set of benchmark functions. Furthermore, and perhaps most important, we show that MO-HillVallEA is capable of obtaining and maintaining multiple approximation sets simultaneously over time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge