Real Elliptically Skewed Distributions and Their Application to Robust Cluster Analysis
Paper and Code
Jun 30, 2020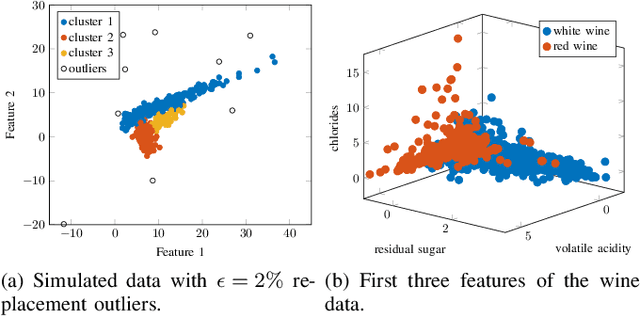
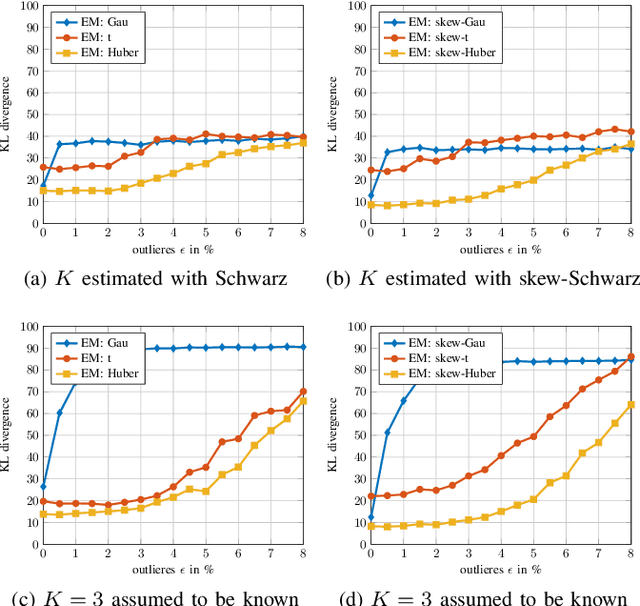
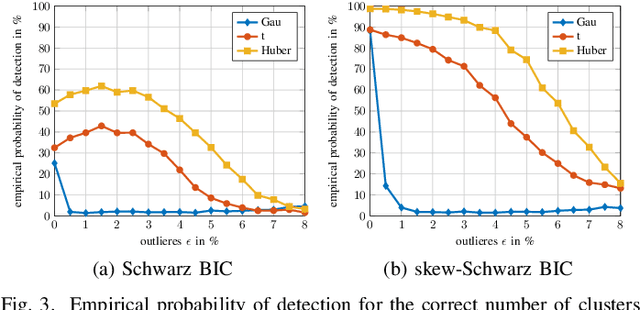
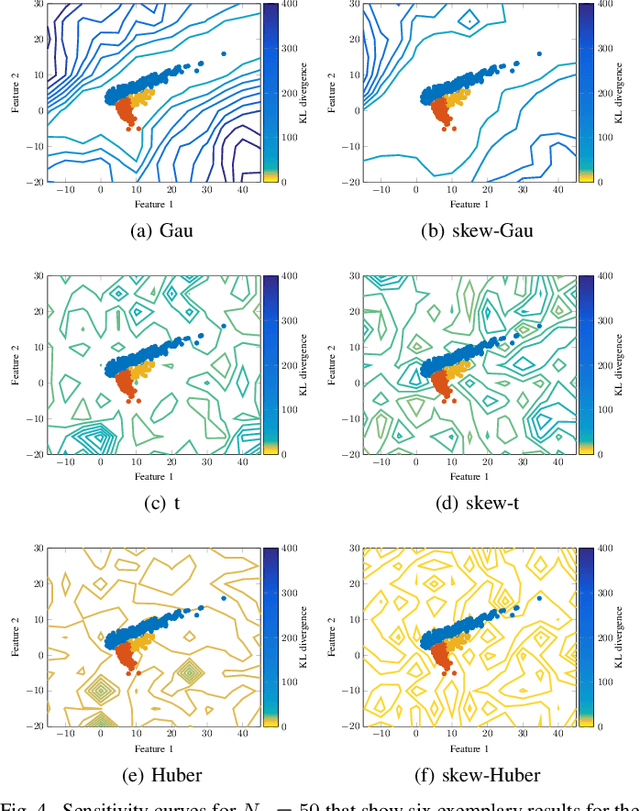
This article proposes a new class of Real Elliptically Skewed (RESK) distributions and associated clustering algorithms that allow for integrating robustness and skewness into a single unified cluster analysis framework. Non-symmetrically distributed and heavy-tailed data clusters have been reported in a variety of real-world applications. Robustness is essential because a few outlying observations can severely obscure the cluster structure. The RESK distributions are a generalization of the Real Elliptically Symmetric (RES) distributions. To estimate the cluster parameters and memberships, we derive an expectation maximization (EM) algorithm for arbitrary RESK distributions. Special attention is given to a new robust skew-Huber M-estimator, which is also the maximum likelihood estimator (MLE) for the skew-Huber distribution that belongs to the RESK class. Numerical experiments on simulated and real-world data confirm the usefulness of the proposed methods for skewed and heavy-tailed data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge