RBM-Flow and D-Flow: Invertible Flows with Discrete Energy Base Spaces
Paper and Code
Jan 28, 2021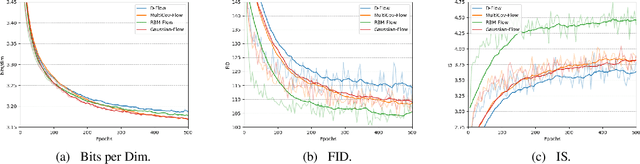



Efficient sampling of complex data distributions can be achieved using trained invertible flows (IF), where the model distribution is generated by pushing a simple base distribution through multiple non-linear bijective transformations. However, the iterative nature of the transformations in IFs can limit the approximation to the target distribution. In this paper we seek to mitigate this by implementing RBM-Flow, an IF model whose base distribution is a Restricted Boltzmann Machine (RBM) with a continuous smoothing applied. We show that by using RBM-Flow we are able to improve the quality of samples generated, quantified by the Inception Scores (IS) and Frechet Inception Distance (FID), over baseline models with the same IF transformations, but with less expressive base distributions. Furthermore, we also obtain D-Flow, an IF model with uncorrelated discrete latent variables. We show that D-Flow achieves similar likelihoods and FID/IS scores to those of a typical IF with Gaussian base variables, but with the additional benefit that global features are meaningfully encoded as discrete labels in the latent space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge