Rapid Feature Evolution Accelerates Learning in Neural Networks
Paper and Code
May 29, 2021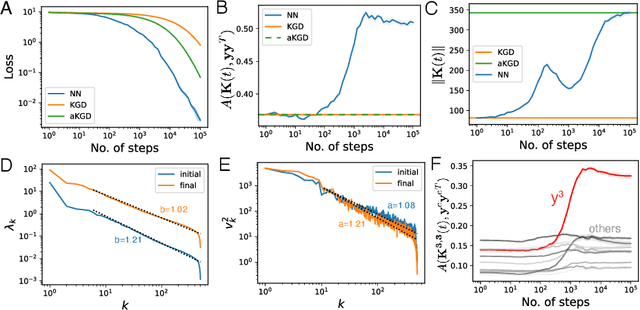
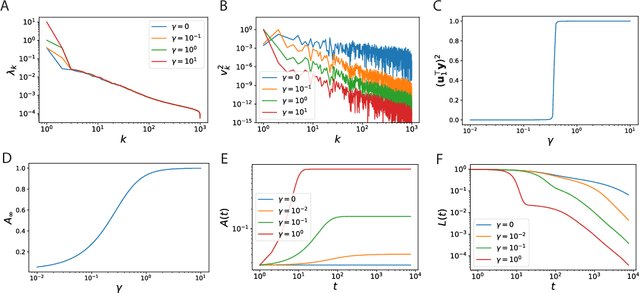
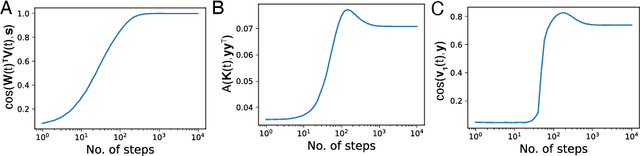
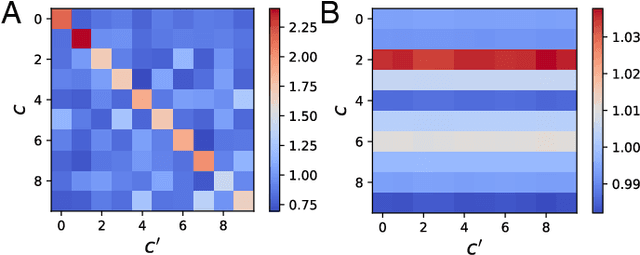
Neural network (NN) training and generalization in the infinite-width limit are well-characterized by kernel methods with a neural tangent kernel (NTK) that is stationary in time. However, finite-width NNs consistently outperform corresponding kernel methods, suggesting the importance of feature learning, which manifests as the time evolution of NTKs. Here, we analyze the phenomenon of kernel alignment of the NTK with the target functions during gradient descent. We first provide a mechanistic explanation for why alignment between task and kernel occurs in deep linear networks. We then show that this behavior occurs more generally if one optimizes the feature map over time to accelerate learning while constraining how quickly the features evolve. Empirically, gradient descent undergoes a feature learning phase, during which top eigenfunctions of the NTK quickly align with the target function and the loss decreases faster than power law in time; it then enters a kernel gradient descent (KGD) phase where the alignment does not improve significantly and the training loss decreases in power law. We show that feature evolution is faster and more dramatic in deeper networks. We also found that networks with multiple output nodes develop separate, specialized kernels for each output channel, a phenomenon we termed kernel specialization. We show that this class-specific alignment is does not occur in linear networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge