Ranking and Combining Latent Structured Predictive Scores without Labeled Data
Paper and Code
Aug 14, 2024


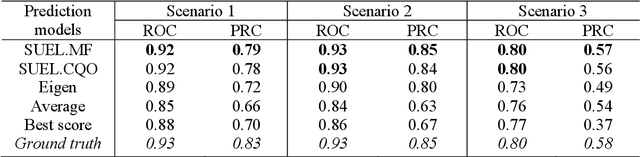
Combining multiple predictors obtained from distributed data sources to an accurate meta-learner is promising to achieve enhanced performance in lots of prediction problems. As the accuracy of each predictor is usually unknown, integrating the predictors to achieve better performance is challenging. Conventional ensemble learning methods assess the accuracy of predictors based on extensive labeled data. In practical applications, however, the acquisition of such labeled data can prove to be an arduous task. Furthermore, the predictors under consideration may exhibit high degrees of correlation, particularly when similar data sources or machine learning algorithms were employed during their model training. In response to these challenges, this paper introduces a novel structured unsupervised ensemble learning model (SUEL) to exploit the dependency between a set of predictors with continuous predictive scores, rank the predictors without labeled data and combine them to an ensembled score with weights. Two novel correlation-based decomposition algorithms are further proposed to estimate the SUEL model, constrained quadratic optimization (SUEL.CQO) and matrix-factorization-based (SUEL.MF) approaches. The efficacy of the proposed methods is rigorously assessed through both simulation studies and real-world application of risk genes discovery. The results compellingly demonstrate that the proposed methods can efficiently integrate the dependent predictors to an ensemble model without the need of ground truth data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge