Randomized Exploration is Near-Optimal for Tabular MDP
Paper and Code
Feb 19, 2021
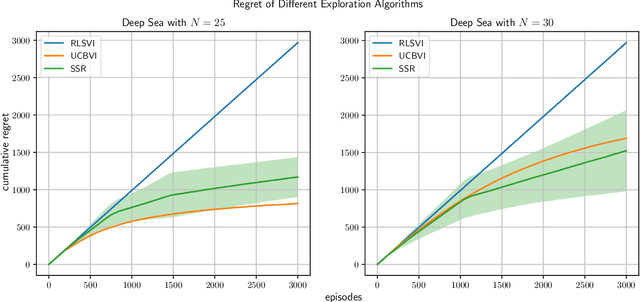
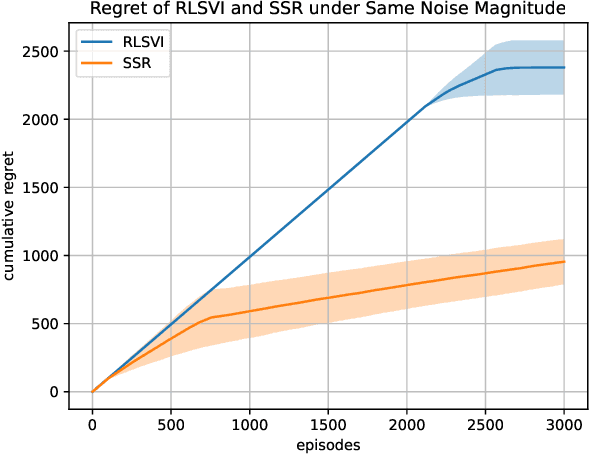
We study exploration using randomized value functions in Thompson Sampling (TS)-like algorithms in reinforcement learning. This type of algorithms enjoys appealing empirical performance. We show that when we use 1) a single random seed in each episode, and 2) a Bernstein-type magnitude of noise, we obtain a worst-case $\widetilde{O}\left(H\sqrt{SAT}\right)$ regret bound for episodic time-inhomogeneous Markov Decision Process where $S$ is the size of state space, $A$ is the size of action space, $H$ is the planning horizon and $T$ is the number of interactions. This bound polynomially improves all existing bounds for TS-like algorithms based on randomized value functions, and for the first time, matches the $\Omega\left(H\sqrt{SAT}\right)$ lower bound up to logarithmic factors. Our result highlights that randomized exploration can be near-optimal, which was previously only achieved by optimistic algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge