Random Forest regression for manifold-valued responses
Paper and Code
Feb 15, 2017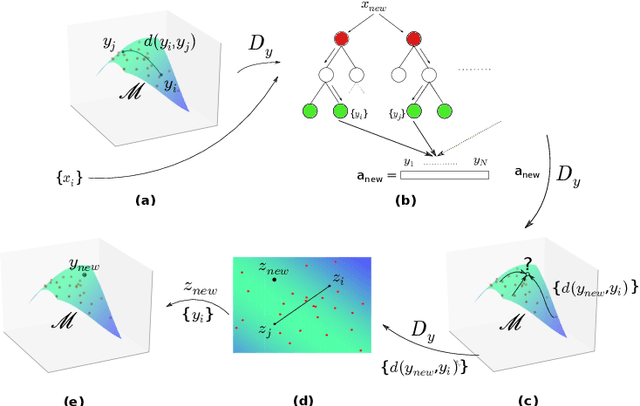

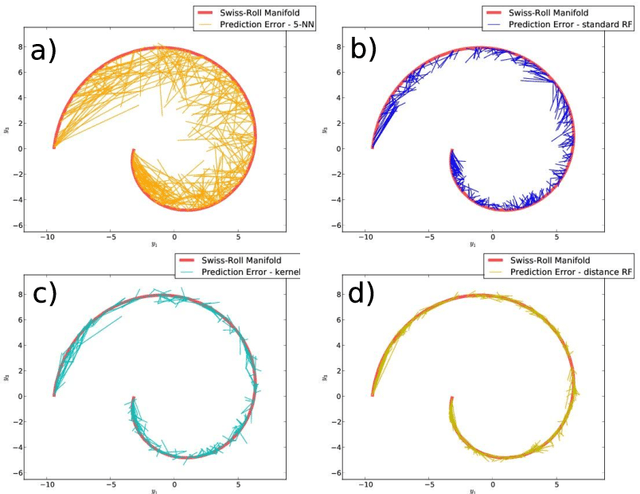

An increasing array of biomedical and computer vision applications requires the predictive modeling of complex data, for example images and shapes. The main challenge when predicting such objects lies in the fact that they do not comply to the assumptions of Euclidean geometry. Rather, they occupy non-linear spaces, a.k.a. manifolds, where it is difficult to define concepts such as coordinates, vectors and expected values. In this work, we construct a non-parametric predictive methodology for manifold-valued objects, based on a distance modification of the Random Forest algorithm. Our method is versatile and can be applied both in cases where the response space is a well-defined manifold, but also when such knowledge is not available. Model fitting and prediction phases only require the definition of a suitable distance function for the observed responses. We validate our methodology using simulations and apply it on a series of illustrative image completion applications, showcasing superior predictive performance, compared to various established regression methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge