Radial Bayesian Neural Networks: Robust Variational Inference In Big Models

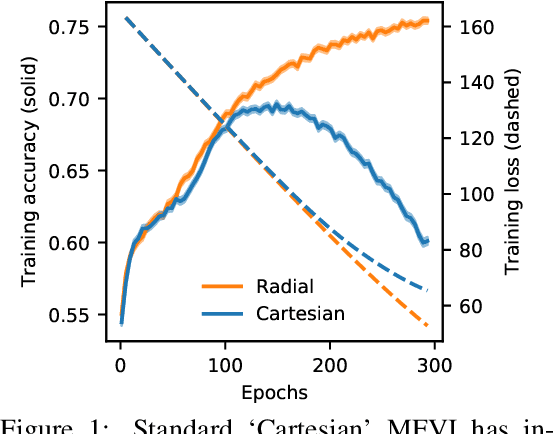
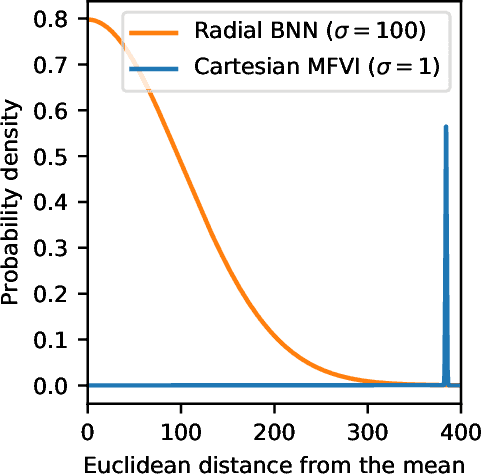
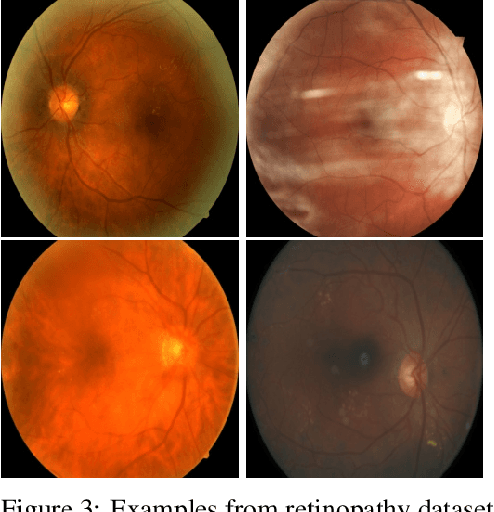
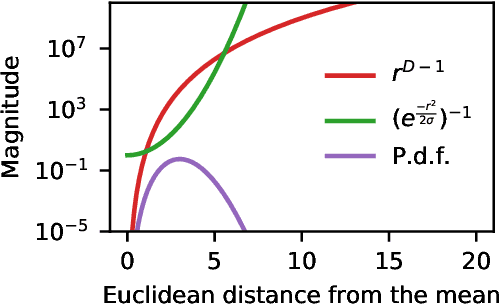
We propose Radial Bayesian Neural Networks: a variational distribution for mean field variational inference (MFVI) in Bayesian neural networks that is simple to implement, scalable to large models, and robust to hyperparameter selection. We hypothesize that standard MFVI fails in large models because of a property of the high-dimensional Gaussians used as posteriors. As variances grow, samples come almost entirely from a `soap-bubble' far from the mean. We show that the ad-hoc tweaks used previously in the literature to get MFVI to work served to stop such variances growing. Designing a new posterior distribution, we avoid this pathology in a theoretically principled way. Our distribution improves accuracy and uncertainty over standard MFVI, while scaling to large data where most other VI and MCMC methods struggle. We benchmark Radial BNNs in a real-world task of diabetic retinopathy diagnosis from fundus images, a task with ~100x larger input dimensionality and model size compared to previous demonstrations of MFVI.