Quaternion kinematics for the error-state Kalman filter
Paper and Code
Nov 03, 2017
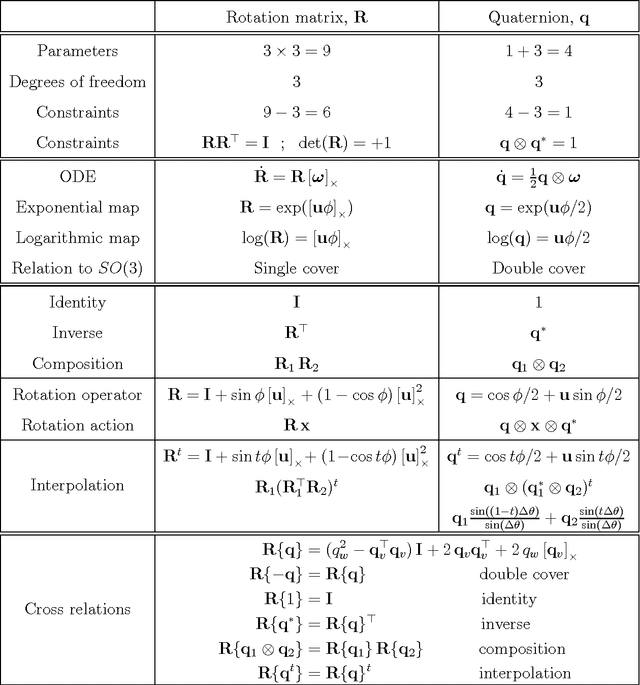


This article is an exhaustive revision of concepts and formulas related to quaternions and rotations in 3D space, and their proper use in estimation engines such as the error-state Kalman filter. The paper includes an in-depth study of the rotation group and its Lie structure, with formulations using both quaternions and rotation matrices. It makes special attention in the definition of rotation perturbations, derivatives and integrals. It provides numerous intuitions and geometrical interpretations to help the reader grasp the inner mechanisms of 3D rotation. The whole material is used to devise precise formulations for error-state Kalman filters suited for real applications using integration of signals from an inertial measurement unit (IMU).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge