Quantum diffusion map for nonlinear dimensionality reduction
Paper and Code
Jun 14, 2021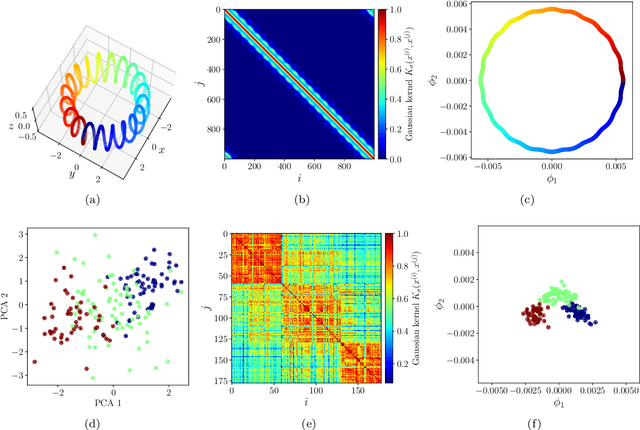

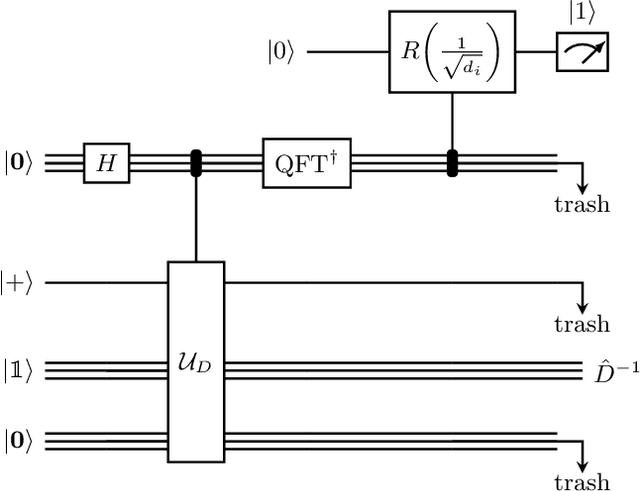

Inspired by random walk on graphs, diffusion map (DM) is a class of unsupervised machine learning that offers automatic identification of low-dimensional data structure hidden in a high-dimensional dataset. In recent years, among its many applications, DM has been successfully applied to discover relevant order parameters in many-body systems, enabling automatic classification of quantum phases of matter. However, classical DM algorithm is computationally prohibitive for a large dataset, and any reduction of the time complexity would be desirable. With a quantum computational speedup in mind, we propose a quantum algorithm for DM, termed quantum diffusion map (qDM). Our qDM takes as an input N classical data vectors, performs an eigen-decomposition of the Markov transition matrix in time $O(\log^3 N)$, and classically constructs the diffusion map via the readout (tomography) of the eigenvectors, giving a total runtime of $O(N^2 \text{polylog}\, N)$. Lastly, quantum subroutines in qDM for constructing a Markov transition operator, and for analyzing its spectral properties can also be useful for other random walk-based algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge