Quantum Computing based Hybrid Solution Strategies for Large-scale Discrete-Continuous Optimization Problems
Paper and Code
Oct 29, 2019

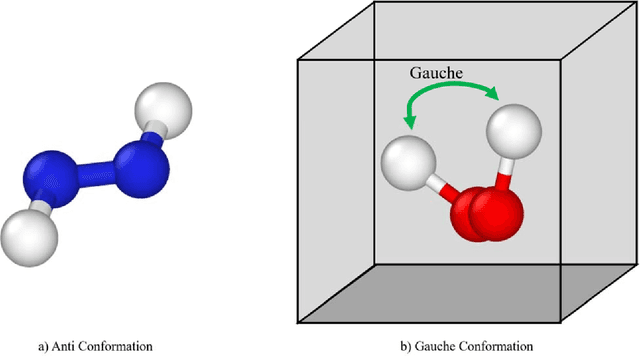

Quantum computing (QC) has gained popularity due to its unique capabilities that are quite different from that of classical computers in terms of speed and methods of operations. This paper proposes hybrid models and methods that effectively leverage the complementary strengths of deterministic algorithms and QC techniques to overcome combinatorial complexity for solving large-scale mixed-integer programming problems. Four applications, namely the molecular conformation problem, job-shop scheduling problem, manufacturing cell formation problem, and the vehicle routing problem, are specifically addressed. Large-scale instances of these application problems across multiple scales ranging from molecular design to logistics optimization are computationally challenging for deterministic optimization algorithms on classical computers. To address the computational challenges, hybrid QC-based algorithms are proposed and extensive computational experimental results are presented to demonstrate their applicability and efficiency. The proposed QC-based solution strategies enjoy high computational efficiency in terms of solution quality and computation time, by utilizing the unique features of both classical and quantum computers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge