Quantitative Susceptibility Map Reconstruction Using Annihilating Filter-based Low-Rank Hankel Matrix Approach
Paper and Code
Apr 25, 2018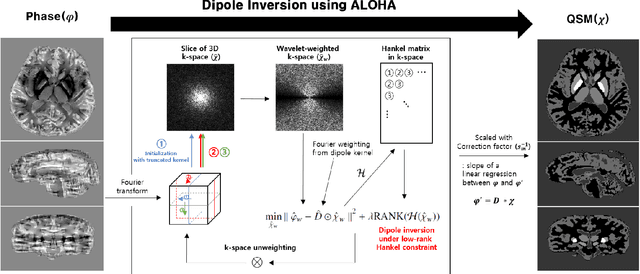
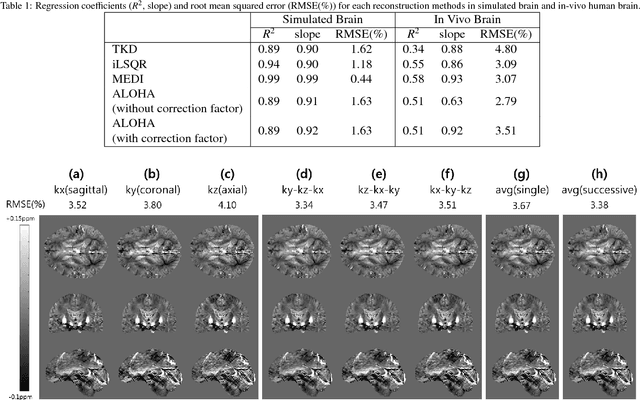


Quantitative susceptibility mapping (QSM) inevitably suffers from streaking artifacts caused by zeros on the conical surface of the dipole kernel in k-space. This work proposes a novel and accurate QSM reconstruction method based on a direct k-space interpolation approach, avoiding problems of over smoothing and streaking artifacts. Inspired by the recent theory of annihilating filter-based low-rank Hankel matrix approach (ALOHA), QSM reconstruction problem is formulated as deconvolution problem under low-rank Hankel matrix constraint in the k-space. To reduce the computational complexity and the memory requirement, the problem is formulated as successive reconstruction of 2-D planes along three independent axes of the 3-D phase image in Fourier domain. Extensive experiments were performed to verify and compare the proposed method with existing QSM reconstruction methods. The proposed ALOHA-QSM effectively reduced streaking artifacts and accurately estimated susceptibility values in deep gray matter structures, compared to the existing QSM methods. Our suggested ALOHA-QSM algorithm successfully solves the three-dimensional QSM dipole inversion problem without additional anatomical information or prior assumption and provides good image quality and quantitative accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge