Pushing the Envelope: From Discrete to Continuous Movements in Multi-Agent Path Finding via Lazy Encodings
Paper and Code
Apr 25, 2020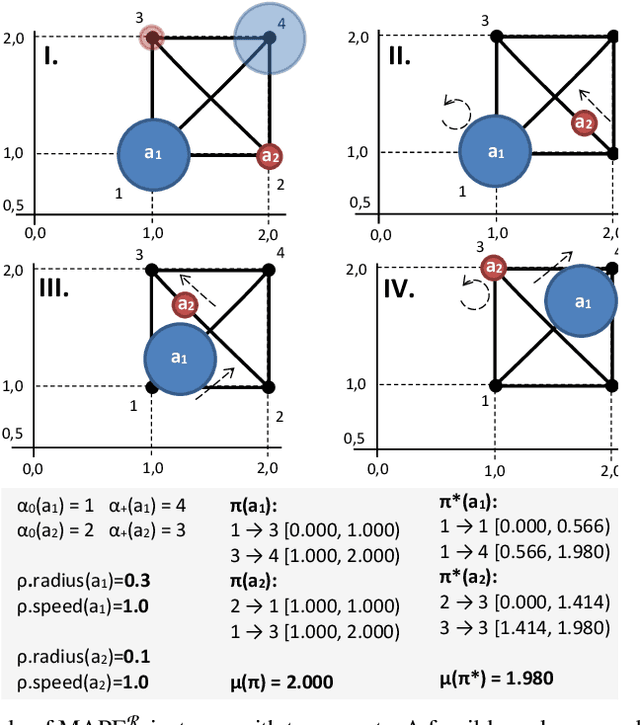
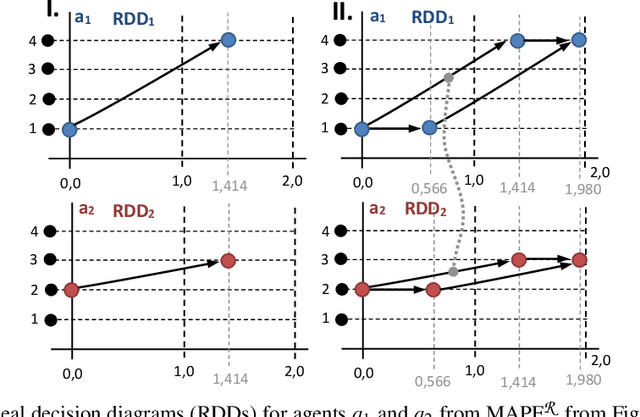
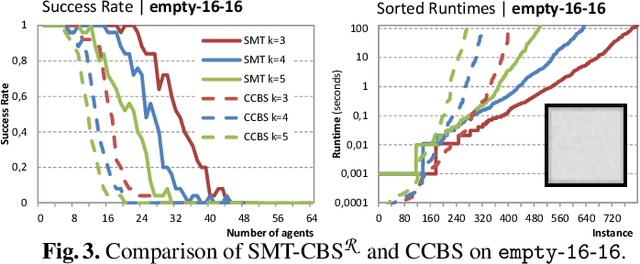
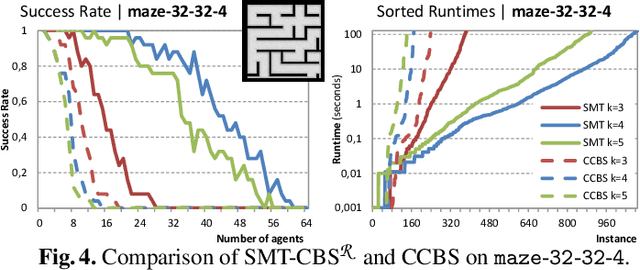
Multi-agent path finding in continuous space and time with geometric agents MAPF$^\mathcal{R}$ is addressed in this paper. The task is to navigate agents that move smoothly between predefined positions to their individual goals so that they do not collide. We introduce a novel solving approach for obtaining makespan optimal solutions called SMT-CBS$^\mathcal{R}$ based on {\em satisfiability modulo theories} (SMT). The new algorithm combines collision resolution known from conflict-based search (CBS) with previous generation of incomplete SAT encodings on top of a novel scheme for selecting decision variables in a potentially uncountable search space. We experimentally compare SMT-CBS$^\mathcal{R}$ and previous CCBS algorithm for MAPF$^\mathcal{R}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge